Предмет: Математика,
автор: Tamara020971
СРОЧНО!!!!! Математики, очень нужна Ваша помощь!
Надо не только ответ, нужно решение. Пожалуйста!!!
Решите неравенство:
3^x + 2 - 28⦁3^0,5x + 3 ≥0
Заранее большое спасибо!!!
Приложения:
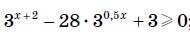
Ответы
Автор ответа:
1
Ответ:
Показательное неравенство .
Сделаем замену : .
Решим квадратное неравенство .
Решением неравенства будет объединение множеств .
Перейдём к старой переменной .
Так как показательная функция возрастающая , то сохранится знак между аргументами .
Ответ: .
Приложения:

Tamara020971:
NNNLLL54? juhjvytqitt Dfv cgfcb,j!!!
NNNLLL54, огромнейшее Вам спасибо!!!!!
Похожие вопросы
Предмет: Алгебра,
автор: levonsymonin
Предмет: Алгебра,
автор: hlyzhingugl
Предмет: Математика,
автор: pdo02084
Предмет: Математика,
автор: 1wertyuiop