Помогите пожалуйста
(нужно именно этап 4, сколько будет решений и какие?)
Заданы основание a и биссектриса b, проведённая к этому основанию, равнобедренного треугольника. Постройте данный равнобедренный треугольник с помощью циркуля и линейки.
При решении обязательно нарисуйте заданные по условию отрезки a и b, которые будут использованы для построения.
Этап 4: исследование. Поясните, сколько решений имеет задача при заданных значениях a и b. Всегда ли задача будет иметь решение при различных значениях a и b?
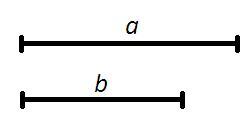
Ответы
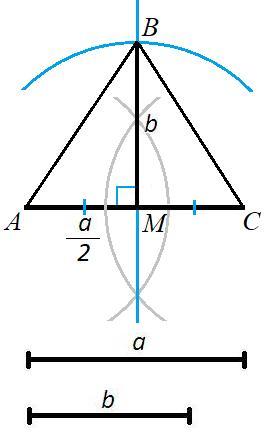
Биссектриса к основанию р/б треугольника является также высотой и медианой.
Строим
- отрезок AC=a
- серединный перпендикуляр к отрезку AC
- M - середина AC
- на серединном перпендикуляре отрезок BM=b
Построили △ABC с основанием a и биссектрисой b к основанию.
△ABC состоит из двух равных треугольников (△ABM=△CBM) с катетами a/2 и b. Два катета однозначно задают треугольник (вспоминаем признак равенства), следовательно △ABM единственный и △ABC единственный. Задача имеет одно решение.
Гипотенуза всегда больше любого катета (т.к. лежит против большего угла). Сумма катетов всегда больше гипотенузы (квадрат суммы катетов больше квадрата гипотенузы на 2ab). Следовательно для любых длин катетов выполняется неравенство треугольника. Задача будет иметь решение при любых положительных a и b.