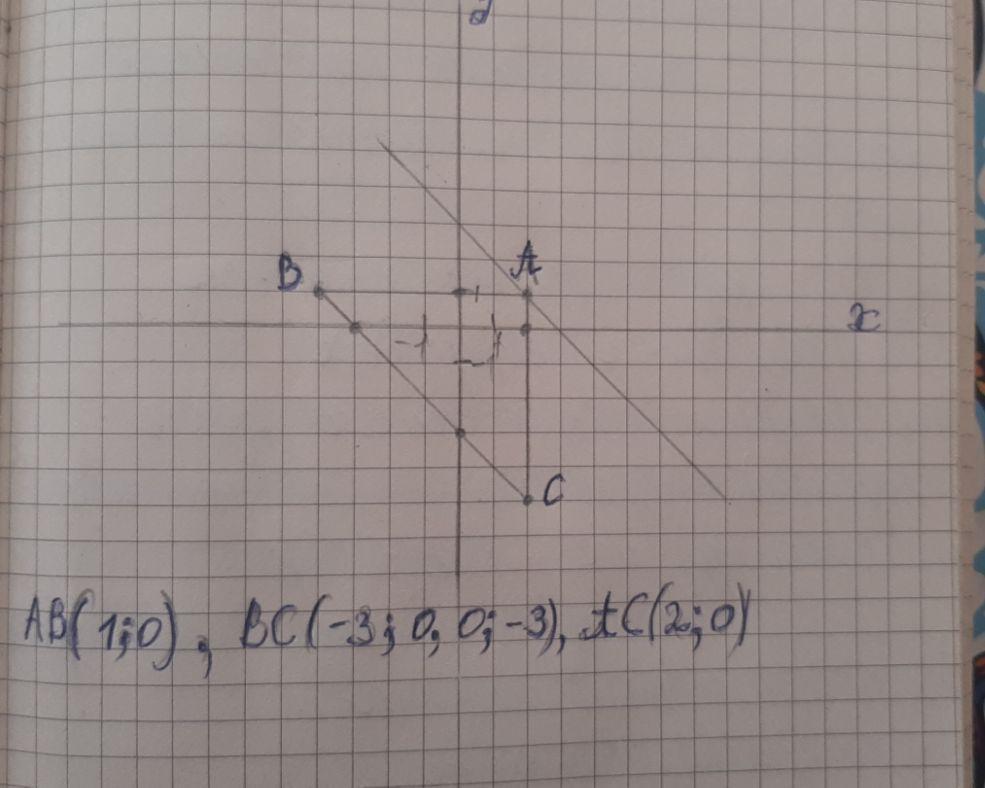
Побудувати на координатній площині трикутник АВС, якщо:
A(2:1), B(-4; 1), C(2:-5).
а)Побудувати через точку А пряму паралельну стороні ВС, і пряму перпендикулярну до сторони ВС
с) Знайти координати точок перетн- сторін трикутника АВС з осями
координат.
Ответы
Ответ:
Для побудови трикутника АВС на координатній площині і знаходження додаткових прямих та точок перетину з осями координат, використаємо надані координати точок A(2,1), B(-4,1), C(2,-5).
a) Щоб побудувати пряму, паралельну стороні ВС через точку А, візьмемо точку D, яка матиме таку саму ординату (y-координату) як точка A і ту саму абсцису (x-координату) як точка C. Точка D буде мати координати D(2,-5). Пряма, що проходить через точки A та D, буде паралельна стороні ВС.
b) Щоб побудувати пряму, перпендикулярну до сторони ВС через точку А, візьмемо середину сторони ВС. Середина сторони ВС буде мати координати E((-4+2)/2, (1-5)/2) = (-1,-2). Пряма, що проходить через точки А та Е, буде перпендикулярна стороні ВС.
c) Щоб знайти координати точок перетину сторін трикутника АВС з осями координат, вирішимо рівняння прямих, що утворюють сторони трикутника, з осями.
Сторона АВ: Пряма AB має рівняння y = 1, оскільки точки A і B мають однакову ординату.
Перетин з віссю ОХ (ось абсцис): Підставимо y = 0 в рівняння прямої AB:
0 = 1
Це не має розв'язків, тому сторона АВ не перетинає вісь ОХ.
Перетин з віссю ОY (ось ординат): Оскільки точка A має ординату 1, то точка A(0,1) перетинає вісь ОY.
Сторона ВС: Рівняння прямої BC можна знайти, використовуючи координати точок B і C:
y = (1-(-5))/(-4-2) * (x - (-4)) + 1
y = 6/6 * (x + 4) + 1
y = x + 5
Перетин з віссю ОХ: Підставимо y =
Пошаговое объяснение:
Відповідь:
надеюсь помог
удачи)