Предмет: Алгебра,
автор: Lisikity
ДУЖЕ ПРОШУ У МЕНЕ МАЛО ЧАСУ!
доведіть тотожність (a/a-3+10/a-3+25/a^2-3a):(5/a^2+2/a+1/5)=5a/a-3
Приложения:
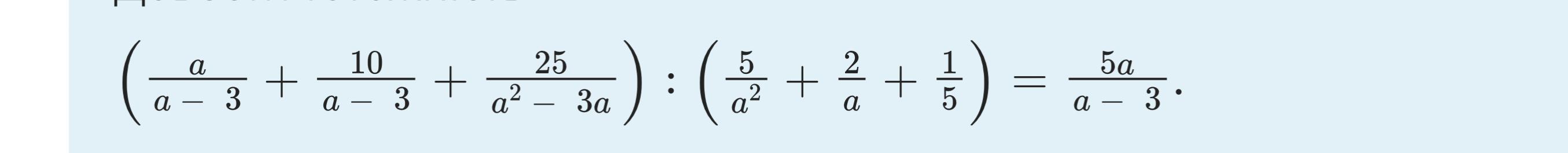
Ответы
Автор ответа:
2
Ответ:
Почнемо з лівого боку:
(a/a-3 + 10/a-3 + 25/a^2-3a) / (5/a^2 + 2/a + 1/5)
За допомогою знаходження спільного знаменника складаємо дроби в чисельнику:
((a+10+a^2-3a*10)/((a-3)*(a^2-3a))) / (5a^2*(a-3)/(a^2+2a*5+a*5*2))
Скорочуємо спільні множники:
((a+10-20a)/((a-3)*(a^2-3a))) / (5a^2*(a-3)/(a+5)^2)
Ділимо на дріб в знаменнику:
(a+10-20a) / (5a^2(a-3)/(a+5)^2) * ((a+5)^2 / 1)
Зменшуємо вираз в чисельнику:
(10-19a) / (5a^2(a-3)) * (a+5)^2
Розв’язуємо дужки в знаменнику:
(10-19a) / (5a^2(a-3)) * (a+5)*(a+5)
Скорочуємо спільні множники:
(2-19/5) / (a-3) * (a+5)
(1/5) / (a-3) * (a+5)
1 / (5(a-3)) * (a+5)
Тепер зведемо праву частину до такого ж виду:
5a/(a-3)
Отже, ми довели, що ліва і права частини тотожні.
Объяснение:
Не дуже шару але якось так
Lisikity:
БОЖЕ ТЫ ВЫРУЧИЛ СПВСИБО БОЛЬШОЕ
/-це ?
Ты имеешь ввиду что это означает? Если да то это знак деление
Ти можеш ще допомогти в профілі питання
А на які питання ще?
Похожие вопросы
Предмет: Информатика,
автор: nuiaoebs
Предмет: География,
автор: arstanbekova422
Предмет: Английский язык,
автор: kiticenkodavid136
Предмет: Алгебра,
автор: ArTema10
Предмет: Русский язык,
автор: klsjfkjshfasjhddfsf