Question

Будь ласка поможіть !!!! . У прямокутний трикутник вписао коло. Точка дотику поділяє один з катетів на відрізки завдовжки 3см і 5 см, рахуючи від вершини прямого кута. Знайдіть гіпотенузу і другий катет трикутника.

Answer 1

Ответ:

Гипотенуза и второй катет равны 17 см и 15 см соответственно.

Объяснение:

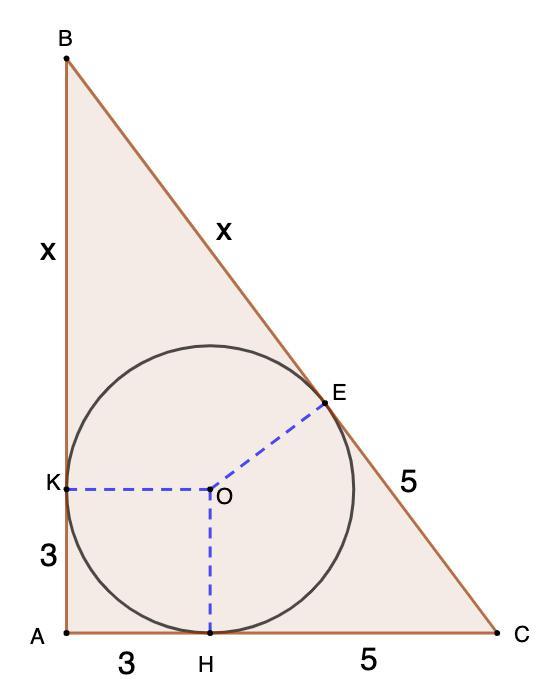
В прямоугольный треугольник вписан круг. Точка соприкосновения разделяет один из катетов на отрезки длиной 3 см и 5 см, считая от вершины прямого угла. Найдите гипотенузу и второй катет треугольника.

Дано: ΔАВС - прямоугольный;

Окр.О - вписана в ΔАВС;

К, Е и Н - точки касания;

АН = 3 см; НС = 5 см.

Найти: АВ и ВС.

Решение:

• Отрезки касательных, проведенных из одной точки к окружности, равны.

Пусть КВ = х см.

⇒ АН = АК = 3 см;   НС = СЕ = 5 см;   КВ = ВЕ = х см.

Тогда:

АВ = АК + КВ = (3 + х) (см)

ВС = ВЕ + ЕС = (х + 5) (см)

АС = АН + НС = 3 + 5 = 8 (см)

По теореме Пифагора:

ВС² = АВ² + АС²

(х + 5)² = (3 + х)² + 64

х² + 10х + 25 = 9 + 6х + х² + 64

4х = 48     |:4

x = 12

⇒ АВ = 3 + 12 = 15 (см)

ВС = 12 + 5 = 17 (см)