Question

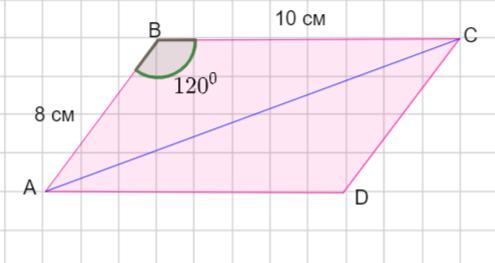
Сторони паралелограма дорівнюють 8 см і 10 см, а один з кутів дорівнює 120°. Знайдіть більшу діагональ паралелограма та площу паралелограма.

Answer 1

Ответ:

Большая диагональ равна 2√61 см. Площадь параллелограмма равна 40√3 см².

Объяснение:

Стороны параллелограмма равны 8 см и 10 см, а один из углов равен 120 °. Найти большую диагональ и площадь параллелограмма.

Пусть дан параллелограмм АВСD , ∠В =120°, АВ = 8см, ВС =10 см.

Большая диагональ лежит напротив большего угла ∠В. Значит, надо найти длину диагонали АС .

Рассмотрим ΔАВС и найдем сторону АС по теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

$AC ^{2} = AB^{2} +BC ^{2} - 2 \cdot AB \cdot BC \cdot cos \angle{} B;\\AC ^{2} = 8^{2} +10 ^{2} - 2 \cdot 8 \cdot 10 \cdot cos120 ^{0}$

Так как $cos(180^{0} -\alpha )=-cos \alpha$  , то $cos120 ^{0} =cos (180^{0} -60^{0} )=-cos 60 ^{0} =-\dfrac{1}{2} .$

$AC ^{2} = 64+100- 2 \cdot 8 \cdot 10 \cdot\left(-\dfrac{1}{2} \right)=164 +80=244;\\AC =\sqrt{244} =\sqrt{4\cdot 61} =2\sqrt{61}$

Тогда большая диагональ равна 2√61 см.

Площадь параллелограмма найдем как произведение сторон параллелограмма на синус угла между ними.

$S =AB \cdot BC \cdot sin \angle{} B;\\S =8 \cdot 10\cdot sin120^{0}$

Так как $sin(180^{0} -\alpha )=sin \alpha$  , то

$sin120 ^{0} =sin (180^{0} -60^{0} )=sin 60 ^{0} =\dfrac{\sqrt{3} }{2} .$

$S =8 \cdot 10\cdot \dfrac{\sqrt{3} }{2} =40\sqrt{3}$

Тогда площадь параллелограмма равна 40√3 см².

#SPJ1