Предмет: Алгебра,
автор: Аноним
Алгебра. Даю 69 балів. потрібно вирішити завдання з максимальним поясненням щоб було усе зрозуміло будь ласка.
з дуже детальним поясненням будь ласка
Приложения:
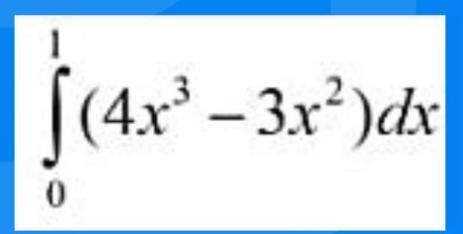
Ответы
Автор ответа:
1
Ответ:
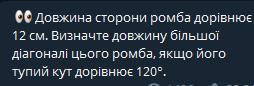
1) Наибольшая диагональ ромба лежит против тупого угла . Её можно вычислить по теореме косинусов , зная что сторона ромба а=12 см , а тупой угол равен 120° .
2) Определённый интеграл вычисляем по формуле Ньютона-Лейбница .
masha01021:
здравствуйте, помогите пожалуйста решить задачу
вы очень добрая , каждый раз помогаете , надеюсь в этот раз тоже....
Похожие вопросы
Предмет: Химия,
автор: dudket2022tiktok
Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Предмет: Английский язык,
автор: ebegzod477
Предмет: Физика,
автор: dimarogachowp32eep