Предмет: Алгебра,
автор: korobkomaksim4
Cрочно допоможіть! Розв'яжіть нерівності.
скрін прікріпив даю 60 балів
Приложения:
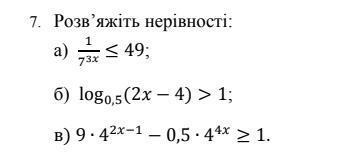
Ответы
Автор ответа:
2
Ответ:
а) х ∈ [-2/3; +∞)
б) x ∈ (2; 2,25)
в) x ∈ [-1/4; 1/2]
Объяснение:
Решить неравенства:
а)
или
Так как основание степени больше 1, то справедливо неравенство:
-3х ≤ 2 |:(-3)
- Если обе части неравенства разделить или умножить на отрицательное число, то знак неравенства перевернется.
х ≥ -2/3
х ∈ [-2/3; +∞)
б)
или
Так как основание логарифма 0 < a < 1, то справедливо неравенство:
2х - 4 < 0,5
Учитывая, что выражение под знаком логарифма положительное, получим систему:
x ∈ (2; 2,25)
в)
Воспользуемся свойствами степеней:
Замена переменной:
Решим неравенство методом интервалов.
Найдем корни уравнения:
2t² - 9t + 4 =0
D = 81 - 32 = 49 ⇒ √D = 7
Определим знаки на интервалах:
⇒ 1/2 ≤ t ≤ 4
Выполним обратную замену:
2 > 1 ⇒
-1 ≤ 4x ≤ 2 |: 4
-1/4 ≤ x ≤ 1/2
x ∈ [-1/4; 1/2]
#SPJ1
ananasikTATA:
Помогите пожалуйста найти производную
Очень Вас прошу
Похожие вопросы
Предмет: Английский язык,
автор: misskaprizz954
Предмет: Английский язык,
автор: nika00667
Предмет: История,
автор: MyrzaIvan131
Предмет: Литература,
автор: d456733
Предмет: Алгебра,
автор: Аноним