Question

ДАМ 100 БАЛІВ!!! 9 завдання

Answer 1

Ответ:

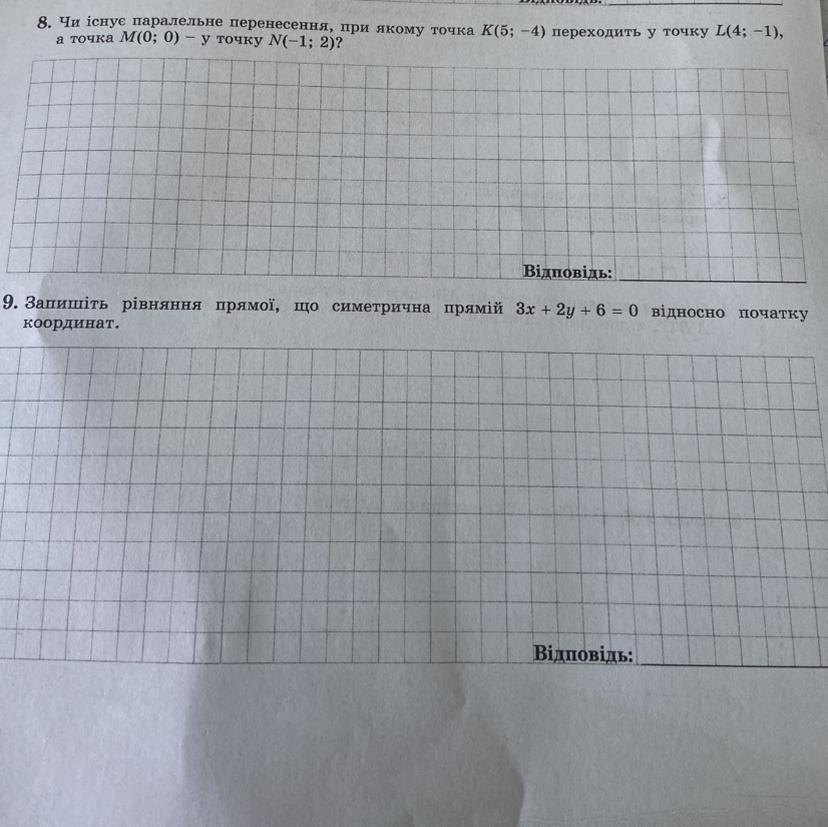
Для запису рівняння прямої, що є симетричною прямій 3x + 2y + 6 = 0 відносно початку координат, можна використати наступний підхід:

Візьмемо оригінальне рівняння 3x + 2y + 6 = 0.

Знайдемо координати точки перетину цієї прямої з віссю OX, де y = 0. Значення x можна знайти, підставивши y = 0 в оригінальне рівняння:

3x + 2(0) + 6 = 0

3x + 6 = 0

3x = -6

x = -2.

Отже, точка перетину з OX має координати (-2, 0).

Оскільки пряма є симетричною відносно початку координат, ми можемо скористатися властивістю симетрії та отримати другу точку на прямій, яка має таку саму відстань від початку координат, але з протилежним знаком. Тобто, друга точка буде мати координати (2, 0).

Використовуючи дві точки (-2, 0) і (2, 0), можна визначити рівняння прямої, використовуючи формулу для визначення рівняння прямої за двома точками:

y - y₁ = m(x - x₁),

де (x₁, y₁) і (x, y) є координатами двох точок на прямій, а m - її нахил (відношення зміни y до зміни x).

Підставимо значення точок (-2, 0) і (2, 0) у формулу:

y - 0 = m(x - (-2))

y = mx + 2m.

Таким чином, рівняння прямої, що є симетричною прямій 3x + 2y + 6 = 0 відносно початку координат, буде:

y = mx + 2m.

Рівняння прямої, що є симетричною прямій 3x + 2y + 6 = 0 відносно початку координат, можна записати у вигляді:

3x + 2y + 6 = -3x - 2y,

або

6x + 4y + 12 = 0.

Отже, рівняння шуканої симетричної прямої є 6x + 4y + 12 = 0.