Предмет: Математика,
автор: azymikato2006
Визначений інтеграл, обчислити інтеграли
Будь ласка допоможіть хоча б щось вирішити :(
Приложения:

Ответы
Автор ответа:
1
Ответ:
Вычисляем определённый интеграл, применяя формулу Ньютона-Лейбница .
Приложения:
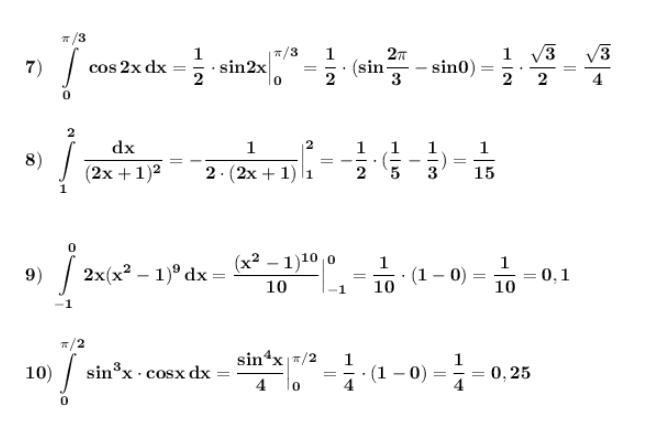
Похожие вопросы
Предмет: Кыргыз тили,
автор: kaatlaura065
Предмет: Алгебра,
автор: offwhiteFriman
Предмет: Математика,
автор: jorayevajasmina7
Предмет: Химия,
автор: soniakoshevaya