Знайдіть рівняння дотичної до графіка функції яка паралельна прямій
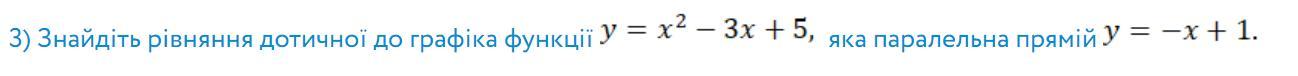
Ответы
Для знаходження рівняння дотичної до графіка функції, яка паралельна прямій у = -x + 1, нам потрібно врахувати, що дві паралельні прямі мають однаковий нахил. Отже, ми повинні знайти похідну функції у = x² - 3x + 5 і зрівняти його з нахилом прямої у = -x + 1.
Похідна функції у = x² - 3x + 5:
у' = 2x - 3
Так як дотична має мати однаковий нахил з прямою у = -x + 1, то ми можемо прирівняти похідну до -1:
2x - 3 = -1
Розв'язуємо це рівняння відносно x:
2x = 2
x = 1
Тепер, щоб знайти відповідне значення у, підставимо x = 1 у вихідне рівняння:
у = (1)² - 3(1) + 5
у = 1 - 3 + 5
у = 3
Таким чином, точка перетину графіка функції з дотичною має координати (1, 3).
Отже, рівняння дотичної до графіка функції у = x² - 3x + 5, яка паралельна прямій у = -x + 1, можна записати у вигляді:
у = -1x + b
Знаходження значення b:
3 = -1(1) + b
3 = -1 + b
b = 4
Таким чином, рівняння дотичної до графіка функції у = x² - 3x + 5, яка паралельна прямій у = -x + 1, є:
у = -x + 4