Предмет: Алгебра,
автор: gameplaychannel
Алгебра. Допоможіть пж. З розв'язанням
Приложения:

Ответы
Автор ответа:
1
Ответ:
Объяснение:
-∞__-__-2__+__0__-__3__+__+∞
↓ ↑ ↓ ↑
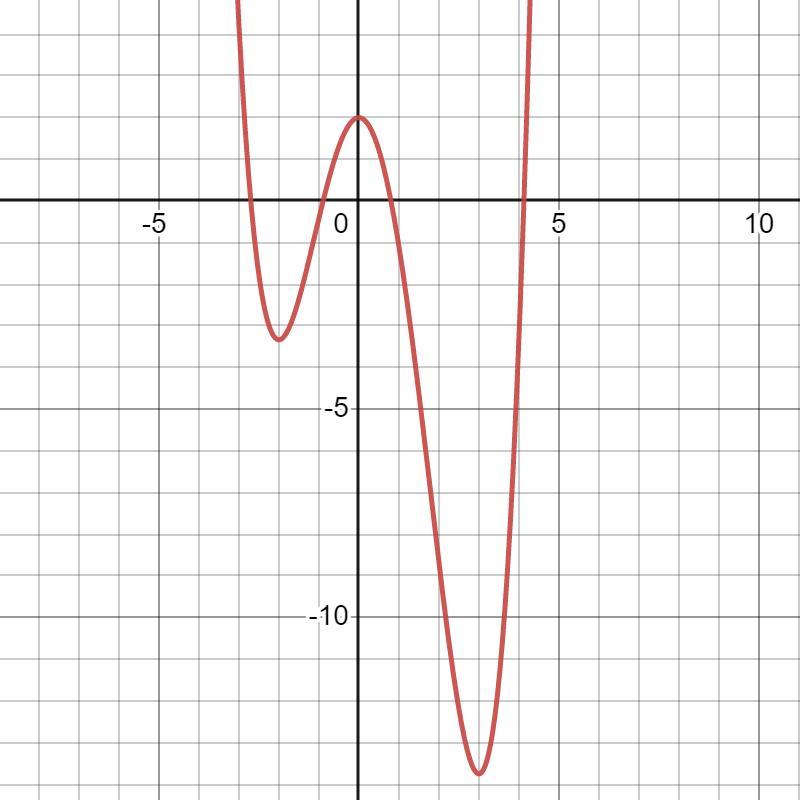
Проміжки зростання функції:
х∈(-2;0)U(3;+∞).
Приложения:
Похожие вопросы