Question

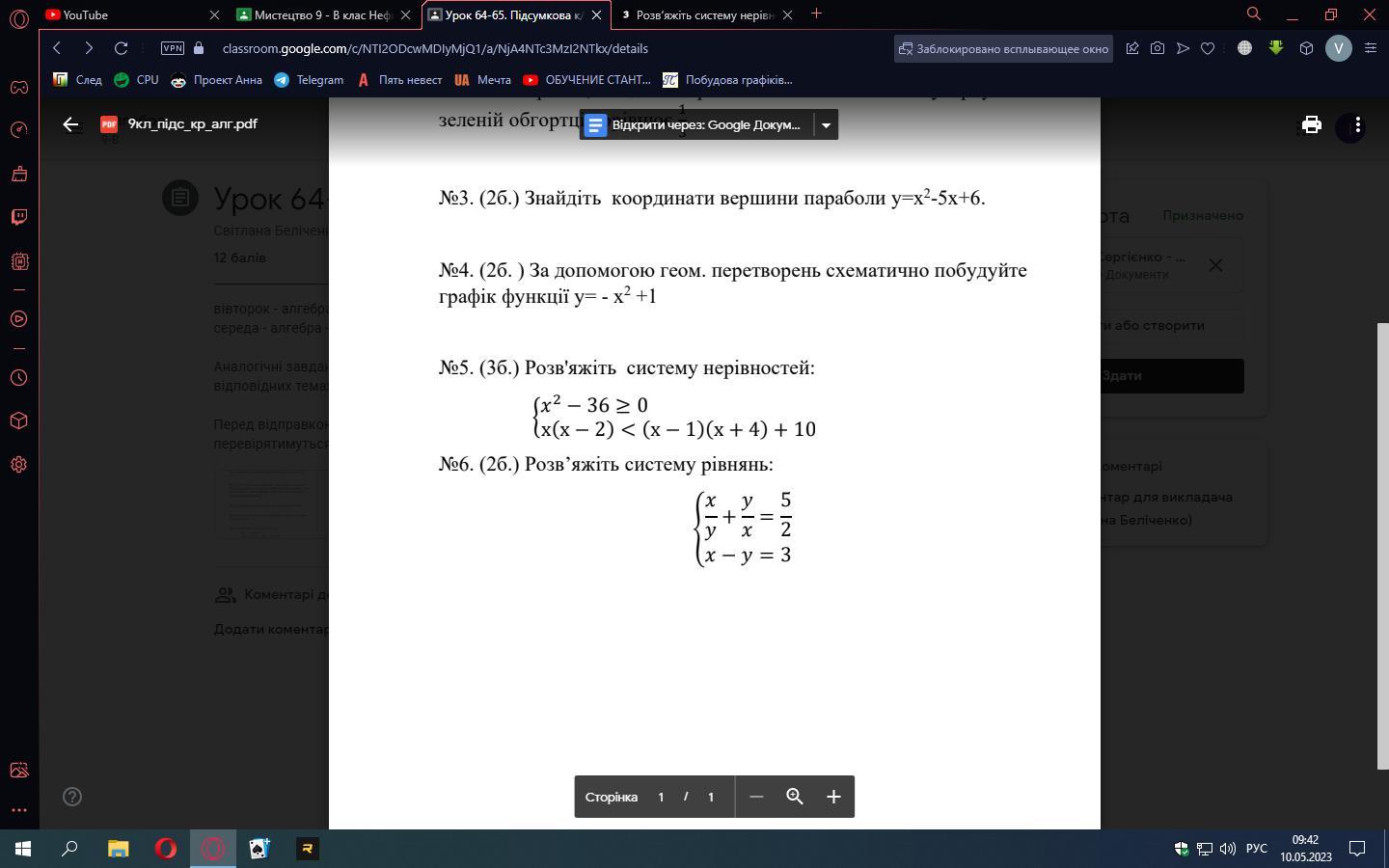
Помогите срочно задание 5 и 6

Answer 1

Ответ:

№5. x ∈[6; +∞)

№6. (x; y) ∈ {(-3; -6), (6; 3)}

Объяснение:

Перевод: №5. Решите систему неравенств:

$\displaystyle \tt \left \{ {{x^2-36\geq 0} \atop {x \cdot (x-2) < (x-1) \cdot (x+4) +10}} \right. .$

№6. Решите систему уравнений:

$\displaystyle \tt \left \{ {{\dfrac{x}{y} +\dfrac{y}{x} =\dfrac{5}{2} } \atop {x -y=3}} \right. .$

Решение. №5. Для решения систему неравенств сначала находим множества решений каждого неравенства системы, а потом определим пересечения этих множеств:

$\displaystyle \tt \left \{ {{x^2-36\geq 0} \atop {x \cdot (x-2) < (x-1) \cdot (x+4) +10}} \right. \\\\\left \{ {{x^2-6^2\geq 0} \atop {x^2-2 \cdot x < x^2+4\cdot x-x-4 +10}} \right. \\\\\left \{ {{(x+6) \cdot (x-6) \geq 0} \atop {0 < 5 \cdot x+6}} \right. \\\\\left \{ {{x \in (-\infty ;-6] \cup [6;+\infty) } \atop {x > -\dfrac{6}{5} }} \right. \\\\\left \{ {{x \in (-\infty ;-6] \cup [6;+\infty) } \atop {x \in (-\dfrac{6}{5} };+\infty)} \right.$

Значит, x ∈[6; +∞).

№6. В системе уравнений (x≠0, y≠0)

$\displaystyle \tt \left \{ {{\dfrac{x}{y} +\dfrac{y}{x} =\dfrac{5}{2} } \atop {x -y=3}} \right.$

сначала решаем первое уравнение методом замены переменных.

$\displaystyle \tt \dfrac{x}{y} +\dfrac{y}{x} =\dfrac{5}{2} , \;\; t=\dfrac{x}{y} \rightarrow \dfrac{1}{t}=\dfrac{y}{x} \\\\t+\dfrac{1}{t}=2,5 \\\\t^2-2,5 \cdot t+1=0\\(t-0,5) \cdot (t-2)=0 \\t-0,5 =0 \lor t-2 =0\\t_1=0,5, t_2=2 \\\dfrac{x}{y} =0,5 \; \lor \; \dfrac{x}{y} =2\\x=0,5 \cdot y \; \lor \; x=2 \cdot y.$

Значит, решаем совокупность систем уравнений, то есть 2 системы уравнений и объединим их решения.

$\displaystyle \tt 1) \; \left \{ {{x=0,5 \cdot y} \atop {x -y=3}} \right. \\\\ \left \{ {{x=0,5 \cdot y} \atop {0,5 \cdot y -y=3}} \right. \\\\\left \{ {{x=0,5 \cdot y} \atop {-0,5 \cdot y =3}} \right. \\\\\left \{ {{x_1=0,5 \cdot (-6)=-3} \atop {y_1 =-6}} \right. .$

$\displaystyle \tt 2) \; \left \{ {{x=2 \cdot y} \atop {x -y=3}} \right. \\\\ \left \{ {{x=2 \cdot y} \atop {2 \cdot y -y=3}} \right. \\\\\left \{ {{x=2 \cdot y} \atop {y =3}} \right. \\\\\left \{ {{x_2=2 \cdot 3=6} \atop {y_2 =3}} \right. .$

Решение системы следующее:

(x; y) ∈ {(-3; -6), (6; 3)}.

#SPJ1