Предмет: Алгебра,
автор: dudarsergej83
умоляю срочно 3. РЕШИТЕ СИСТЕму неравенств: 5x – 12 < 0 2 - 7x+420 13x2
Приложения:
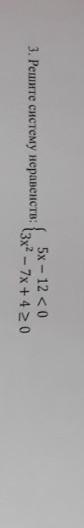
Ответы
Автор ответа:
0
Ответ:
х ∈ (-∞; 1] ∪ [4/3; 12/5).
Объяснение:
Решить систему уравнений:
Решим первое неравенство:
или х ∈ (-∞; 12/5)
Неравенство строгое, поэтому точка будет выколота.
Решим второе неравенство методом интервалов:
Сначала решим уравнение:
Отметим эти точки на числовой оси и определим знаки на промежутках. (см. рис). Решением будут промежутки со знаком "+".
Так как неравенство нестрогое, то данные точки входят в решение.
х ∈ (-∞; 1] ∪ [4/3; +∞)
Объединив решения, получим:
х ∈ (-∞; 1] ∪ [4/3; 12/5).
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: vdelec526
Предмет: Геометрия,
автор: rozovicsergej
Предмет: Биология,
автор: sofik8869
Предмет: Математика,
автор: vasyahaliev
Предмет: Химия,
автор: aliona2527