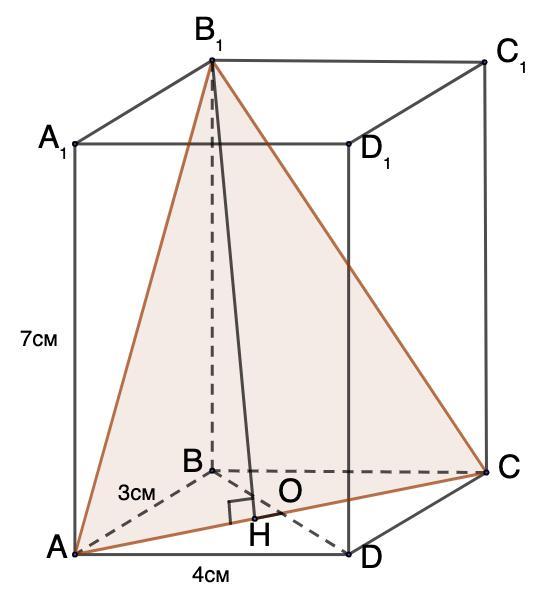
2. СТОРОНЫ прямоугольного параллелепипеда равны 3 см, 4 cm и 7 cm. Найдите площадь сечения, проведенного через концы трёх рёбер, исходящих из одного конца.
Ответы
Ответ:
Площадь сечения равна 18,5 см².
Объяснение:
Стороны прямоугольного параллелепипеда равны 3 см, 4 cм и 7 cм. Найдите площадь сечения, проведенного через концы трёх рёбер, исходящих из одного конца.
Построим сечение.
Возьмем вершину В. Из нее выходят три ребра: ВВ₁, ВА, ВС.
Соединим точки В₁, А и С. Получили искомое сечение.
Дано: ABCDA₁B₁C₁D₁ - прямоугольный параллелепипед;
АВ = 3 см; AD = 4 см; АА₁ = 7 см.
В₁АС - сечение.
Найти: S(В₁АС)
Решение:
Найдем стороны ΔВ₁АС.
Рассмотрим ΔАВ₁В - прямоугольный.
По теореме Пифагора:
АВ₁² = АВ² + ВВ₁² = 9 + 49 = 58 ⇒ АВ₁ = √58 (см)
Рассмотрим ΔВВ₁С - прямоугольный.
По теореме Пифагора:
СВ₁² = ВС² + ВВ₁² = 16 + 49 = 65 ⇒ СВ₁ = √65 (см)
Рассмотрим ΔАВС - прямоугольный.
По теореме Пифагора:
АС² = АВ² + ВС² = 9 + 16 = 25 ⇒ АС = 5 (см)
Проведем высоту ВН.
Рассмотрим ΔАВ₁Н и ΔНВ₁С - прямоугольные.
Выразим В₁Н из каждого треугольника.
Пусть АН = х см, тогда НС = (5 - х) см.
Из ΔАВ₁Н: В₁Н² = АВ₁² - АН² = 58 - х²
Из ΔНВ₁С: В₁Н² = СВ₁² - НС² = 65 - (5 - х)²
Приравняем данные выражения:
58 - х² = 65 - (5 - х)²
58 - х² = 65 - 25 + 10х - х²
10х = 18 |:10
x = 1,8
⇒ В₁Н² = 58 - x² = 58 - 3,24 = 54,76 ⇒ В₁Н = √54,76 = 7,4 (см)
Теперь найдем S(В₁АС).
- Площадь треугольника равна половине произведения высоты на сторону, к которой проведена высота.
Площадь сечения равна 18,5 см².
#SPJ1