Предмет: Алгебра, автор: dariixxqq

БУДЬ ЛАСКА ДОПОМОЖІТЬ!!!!!!

Приложения:

Ответы

Автор ответа: сок111213

$\displaystyle\bf\\ + \left \{ {{4x - 3y = 5} \atop {7x + 3y = 17}} \right. \\ \\4x + 7x = 5 + 17 \\ 11x = 22 \\ x = 22 \div 11 \\ x = 2 \\ \\ 7 \times 2 + 3y = 17 \\ 14 + 3y =1 7 \\ 3y =17 - 14 \\ 3y = 3 \\ = 3 \div 3 \\ y = 1$

Ответ: ( 2 ; 1 )

Автор ответа: Ksfosnc

Ответ: х=2, у=1

Объяснение:

Приложения:

Предыдущий вопрос

Следующий вопрос

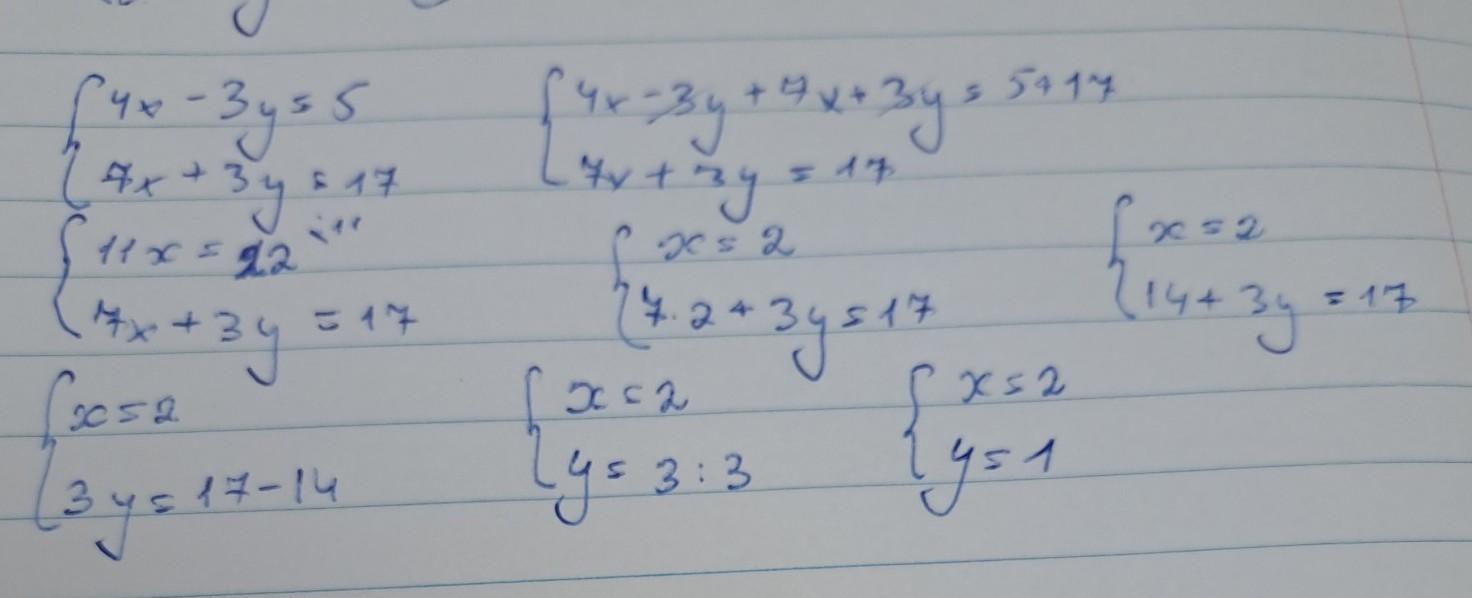
Похожие вопросы

Предмет: География, автор: basenkoruslan21

Оберіть найдрібніший масштаб
1: 2 000
1: 20 000
1: 200 000
1: 2 000 000

2 года назад

Предмет: Алгебра, автор: Аноним

число, большее, чем 2007. (А. Шаповалов)

4. (6-8) Решите ребус РОТОР:СОКОЛ = 3:1. (А. Хачатурян)

5. (6-7) Решите ребус: FOOLS + ROADS = RUSSIA. (К. Кноп)

6. (6-7) На доске было написано равенство. Дежурный по классу успел стереть некоторые цифры (сколько цифр он стёр, неизвестно). На доске осталось:

1127...173×1017...565 = 1126...745.

Могло ли исходное равенство быть верным? (Фольклор)

7. (7-8) На доске выписаны все целые числа от 1 до n. Сеня посчитал, сколько всего цифр выписано. Оказалось, что это число записывается теми же цифрами, что и n, но в обратном порядке. Найдите n, если известно что оно

а) двузначно;

б) трехзначно. (А. Шаповалов)

8. (7-8) Каждая цифра натурального числа N строго больше стоящей слева от нее цифры. Чему равна сумма цифр числа 9N? С.Волчёнков)

9. (7-8) Докажите, что между натуральными числами n и 9n есть натуральное число, чья сумма цифр на 7 больше чем у n. (А. Шаповалов)

10. (7-8) Верно ли, что любое натуральное число, делящееся на 9, отличается от некоторого натурального числа n на сумму цифр этого числа n? (И. Акулич)

11. (8-9) В одну строку без пробелов выписаны числа натурального ряда: 12345678910111213... Далее цифры полученной последовательности попеременно складываются на разные плечи качелей: цифру 1 – на левое плечо, цифру 2 – на правое, цифру 3 – на левое и т.д. Если

2 года назад

Предмет: Французский язык, автор: 6pdsb722tx

Завдання 5 на фото срочно!!!!!!!!!!!!!!!!!!!!!!!

2 года назад

Предмет: Алгебра, автор: kaffikk

Помогите пожалуйста решить

7 лет назад

Предмет: Українська мова, автор: Fack221

Визначте в кожному з речень пряму мову та слова автора.
Перепишіть, розставляючи пропущені розділові знаки.
* Хто ви прапрадіди гукаю.
* Від мами любої в дитинстві почув я вперше ці слова Реве та стогне
Дніпр широкий сердитий вітер завива.

7 лет назад