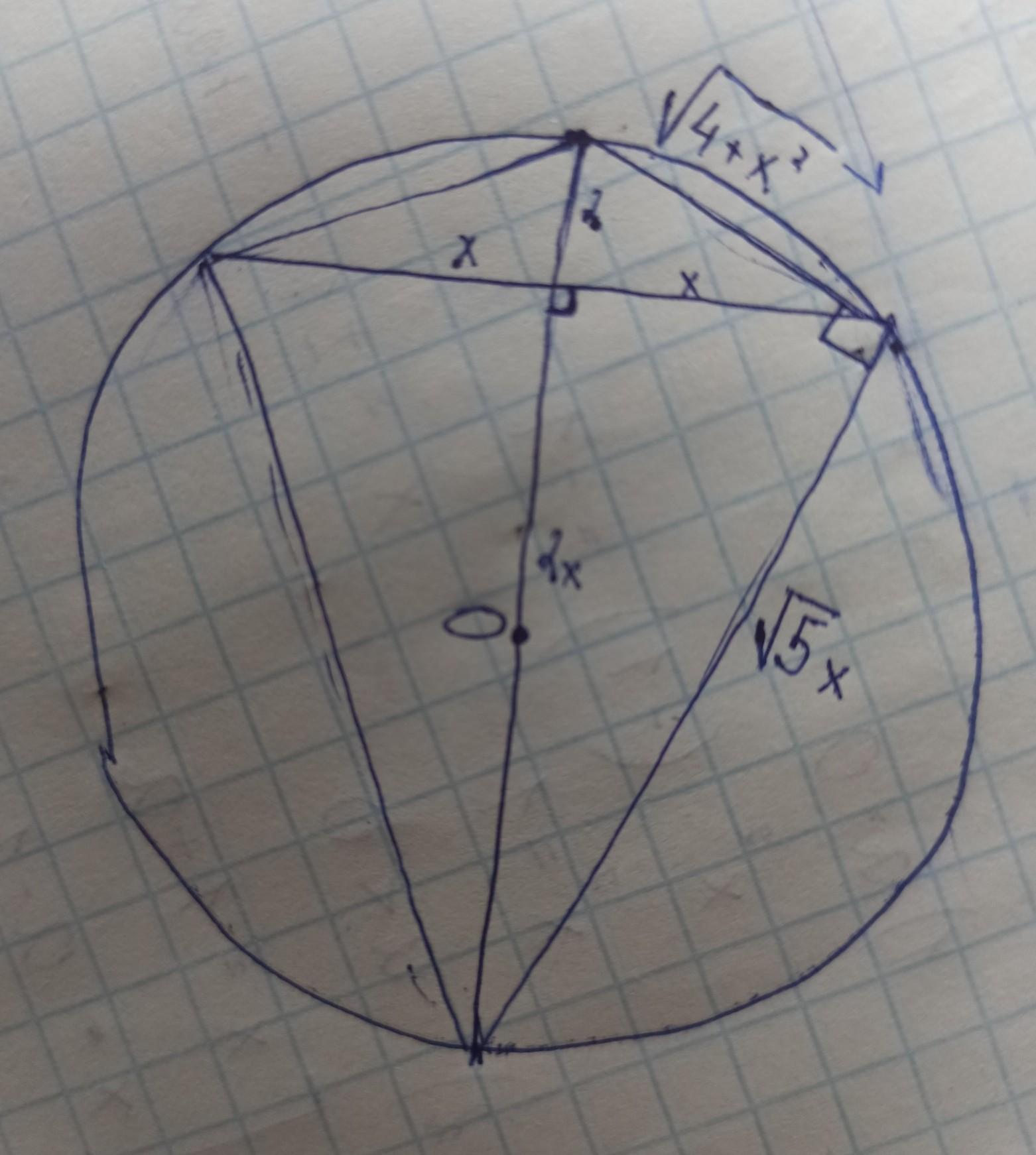В равнобедренном треугольнике высота равна 2, сумма длин основания и высоты равна диаметру описанной окружности. Найти радиус окружности, описанной около этого треугольника. Помогите, пожалуйста.
Ответы
Ответ:
R=5
Объяснение:
На рисунке я изобразил данный в условии треугольник как тупой, но это неважно, ибо на решение это не повлияет
1)Продолжу высоту, новый отрезок будет равен сумме основания и высоты, поскольку продолжение серединного перпендикуляра до точки пересечения с окружностью есть диаметр(высота в условии, думаю, проведена к основанию).
2)Обозначу длину основания за 2x
3)По теореме Пифагора найду по стороне в каждом треугольнике(их размеры уже обозначил на рисунке)
4)Заметим, что между сторонами x√5 и √(4+x²) прямой угол, поскольку он опирается на диаметр
5) Составим уравнение: с одной стороны диаметр равен 2+2x, а с другой его можно найти по Пифагору через найденные раннее стороны
Поскольку сторона не нулевая, то подходит только x=4
Значит диаметр равен 2x+2=8+2=10, а радиус, следовательно, пяти