Предмет: Математика,
автор: grigorenkooleg009
ПомоГИТЕЕЕЕИИИИИ пажэ
Приложения:

Ответы
Автор ответа:
0
Ответ.
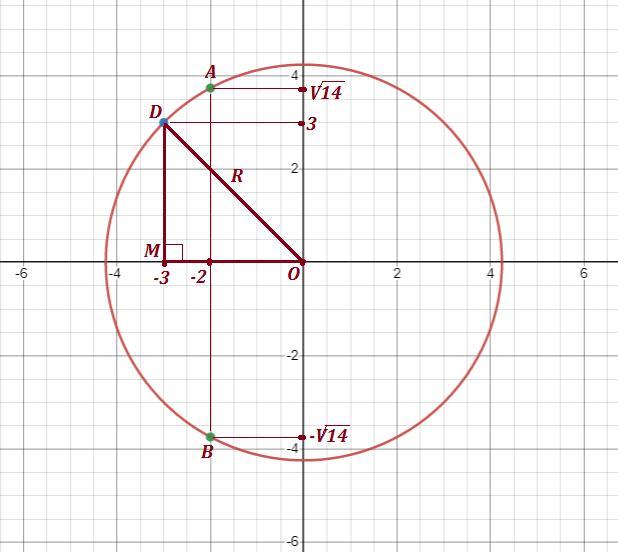
Найдём радиус окружности с центром в точке (0,0), проходящей
через точку D(-3,3) , из треугольника ОМD по теореме Пифагора .
Он равен
.
Уравнение такой окружности имеет вид : .
Точек с абсциссой х= -2 на окружности будет две - точки А и В .
.
Координаты этих точек : .
Приложения:

Похожие вопросы
Предмет: Математика,
автор: noskovasofi48
Предмет: История,
автор: Yumichan68987
Предмет: Физика,
автор: ariyaaa
Предмет: Геометрия,
автор: CONSE458236