Предмет: Математика,
автор: helphelphelp8
допоможіть будь ласочка проінтегрувати безпосередньо
Приложения:
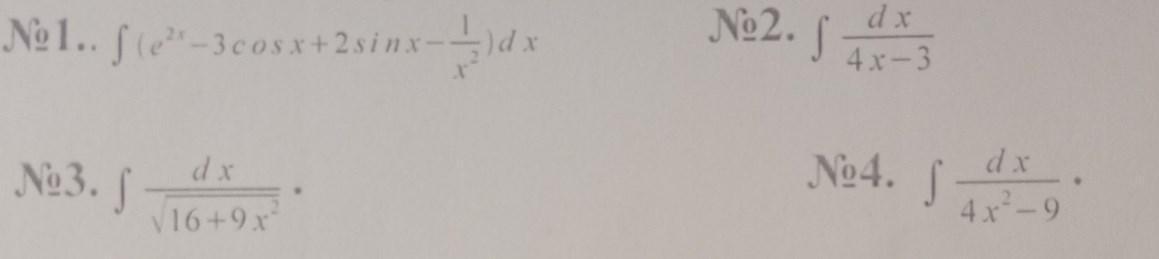
Ответы
Автор ответа:
3
Ответ:
1.
2.
3.
4.
Пошаговое объяснение:
Вычислить интегралы.
Преобразуем интегралы под табличные значения.
Формулы смотри во вложении.
#SPJ1
Приложения:
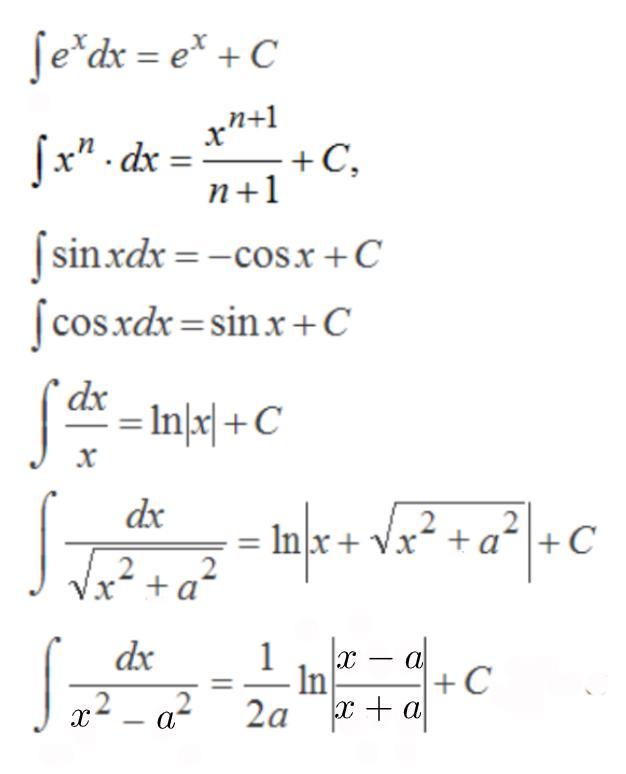
Похожие вопросы
Предмет: Физика,
автор: juliabrosa
Предмет: Физика,
автор: dashenkadasha535
Предмет: Алгебра,
автор: ssuke361
Предмет: Русский язык,
автор: AeroAlex94