Предмет: Математика,
автор: Tamara020971
срочно!!! Уважаемые математики, помогите пожалуйста!!!
Составьте уравнение касательной графика данной функции в точке с абсциссой x0: f(x) = 2/х, х0= -2
(Только пожалуйста с решением).
Заранее большое спасибо!
Приложения:
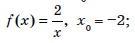
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Составить уравнение касательной:
- Уравнение касательной:
Найдем f(x₀):
Найдем производную:
Теперь составим уравнение касательной:
Tamara020971:
natalyabryukhova, огромнейшее Вам спасибо!!!!
Похожие вопросы
Предмет: Английский язык,
автор: stepanbarkhatov2012
Предмет: Українська література,
автор: Аноним
Предмет: Математика,
автор: 0951364240v
Предмет: Биология,
автор: PrincessAlone
Предмет: Химия,
автор: theann34