Question

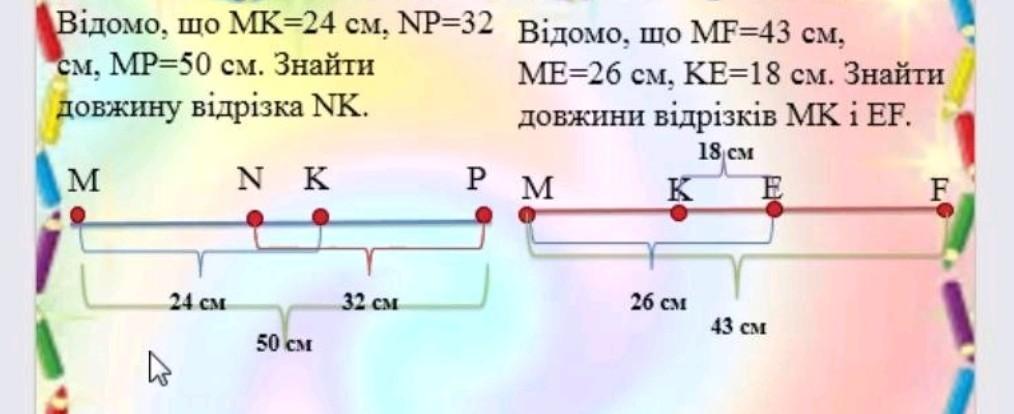
Відомо, що Мк=24 см, NP=32 вiдомо, що МF=43 см, см, MP=50 см. Знайти довжину вiдрiзка NK. N K M A 24 см 50 см 32 cм МЕ=26 см, КЕ=18 см. Знайти довжини відрізків MK і EF. 18 см РМ K 26 см 43 см F​

Answer 1

Ответ:

Для вирішення цієї задачі нам знадобиться використати теорему Піфагора та теорему про перпендикулярність прямих.

Знайдемо спочатку довжину відрізка MK. За теоремою Піфагора для трикутника MNP знаходимо довжину NP:

NP^2 = MP^2 - MN^2 = 50^2 - 24^2 = 2304

NP = √2304 = 48

Тепер візьмемо до уваги трикутник MNK та знайдемо довжину відрізка MK за допомогою теореми Піфагора:

MK^2 = MN^2 + NK^2 = 24^2 + NK^2

Також відомо, що в трикутнику MKN пряма NP є висотою, тому відрізок MK ділиться на дві частини відрізком NK від точки перетину з NP. Позначимо довжину відрізка NK як х.

За теоремою Піфагора для трикутника MNP знаходимо довжину MP:

MP^2 = NP^2 + NM^2 = 48^2 + 24^2 = 2496

MP = √2496 ≈ 49.96

За теоремою Піфагора для трикутника MPK знаходимо довжину PK:

PK^2 = MP^2 - MK^2 = 49.96^2 - 24^2 - x^2

Також відомо, що в трикутнику MEF пряма NK є висотою, тому відрізок EF ділиться на дві частини відрізком NE та KF. Позначимо довжину відрізка EF як у.

За теоремою Піфагора для трикутника MEF знаходимо довжину MF:

MF^2 = ME^2 + EF^2 = 26^2 + u^2

За теоремою Піфагора для трикутника MFK знаходимо довжину FK:

FK^2 = MF^2 - MK^2 = 43^2 - 24^2 - x^2 - u^2

За теоремою Піфагора для трикутника NEK знаходимо довжину NE:

NE^2 = NK^2 - KE^2 = x^2 - 18^2

За теоремою Піфагора для трикутника NKF знаходимо довжину NF:

NF^2 = NE^2 + EF^