Question

Найдите все значения a, при каждом из которых уравнение

$\sqrt{x^{2} - a^{2}} = \sqrt{3x^{2} - (3a + 1)x + a}$

имеет ровно один корень на отрезке [0;1]

Answer 1

Ответ:

(см. объяснение)

Пошаговое объяснение:

$\sqrt{x^2-a^2}=\sqrt{3x^2-(3a+1)x+a}\;\Leftrightarrow\;\left\{\begin{array}{c}x^2-a^2=3x^2-(3a+1)x+a\\x^2-a^2\ge0\end{array}\right;$

Рассмотрим первую строку системы:

$x^2-a^2=3x^2-(3a+1)x+a\\a^2+(1-3x)a+(2x^2-x)=0\\D=(1-3x)^2-4(2x^2-x)=x^2-2x+1=(x-1)^2\\\sqrt{D}=x-1$

$\left[\begin{array}{c}a=\dfrac{3x-1+x-1}{2}\\a=\dfrac{3x-1-x+1}{2}\end{array}\right;\;\;\;\left[\begin{array}{c}a=2x-1\\a=x\end{array}\right;$

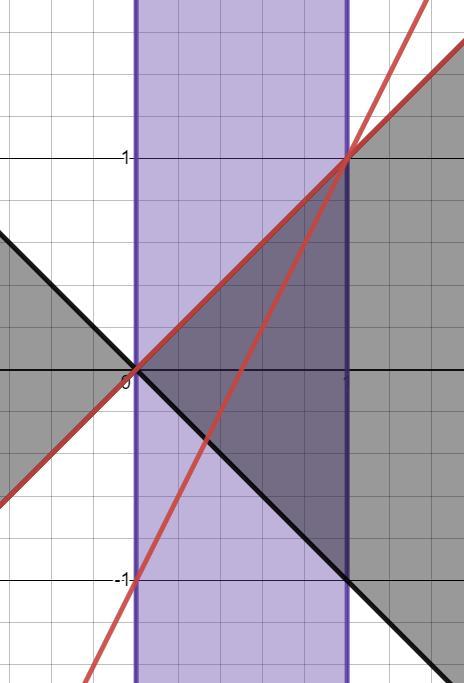
Строим в координатах (x; a) прямые $a=2x-1,\;a=x$ и $a^2-x^2\ge0$.

Получаем то, что в прикрепленном файле (для удобства промежуток $[0;\;1]$ выделен фиолетовым).

Точки пересечения прямых я уверен вы определите - это несложно.

Таким образом, исходное уравнение имеет единственное решение на отрезке $[0;\;1]$ при $a\in\left[-\dfrac{1}{3};\;0\right)\cup\left\{1\right\}$.

Задание выполнено!