ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО
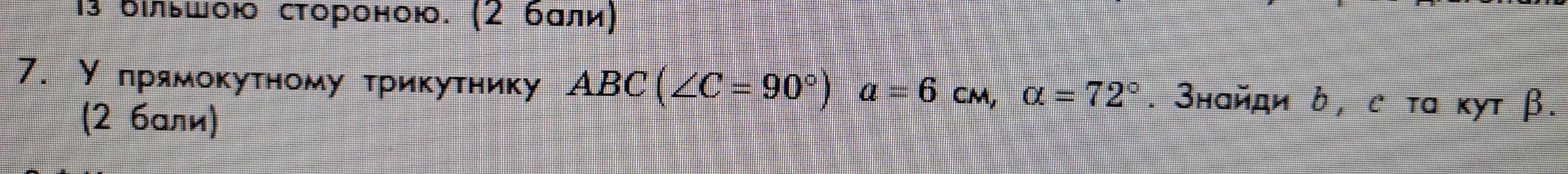
Ответы
Ответ:
Дано: ∆ABC (ZC = 90°), a = 6 см, ∠CAB = 72°
Знацти: b, c, ∠ABC
Розв'язок:
sin(72°) = b/c
cos(72°) = a/c
c = a/cos(72°) ≈ 19.4 см
b = c * sin(72°) ≈ 18.5 см
∠ABC = 180° - ∠ACB - ∠CAB = 180° - 90° - 72° = 18°
Відповідь: b ≈ 18.5 см, c ≈ 19.4 см, ∠ABC = 18°
Объяснение:
Оскільки у вас є прямокутний трикутник ABC з прямим кутом при вершині C (ZC = 90°), де a = 6 см та ∠CAB = 72°, то ви можете використати тригонометричні функції, щоб знайти b та c.
Синус кута CAB дорівнює протилежному катету (b), поділеному на гіпотенузу (c). Таким чином, sin(72°) = b/c. Косинус кута CAB дорівнює прилеглому катету (a), поділеному на гіпотенузу (c). Таким чином, cos(72°) = a/c.
З цих рівнянь ми можемо знайти значення b та c. b = c * sin(72°) та a = c * cos(72°). З другого рівняння ми можемо знайти значення c: c = a/cos(72°). Підставивши значення a = 6 см, ми отримуємо c ≈ 19.4 см.
Тепер ми можемо знайти значення b, підставивши значення c у перше рівняння: b = c * sin(72°) ≈ 18.5 см.
Щоб знайти кут В, ми можемо скористатися тим фактом, що сума кутів у трикутнику дорівнює 180°. Отже, ∠ABC + ∠ACB + ∠CAB = 180°. Ми знаємо, що ∠ACB = 90° та ∠CAB = 72°, отже ∠ABC = 180° - 90° - 72° = 18°.
Отже, у вашому трикутнику b ≈ 18.5 см, c ≈ 19.4 см та ∠ABC = 18°.