3. Укажіть рiвняння, яке можна звести до квадратного. Б) x4 + 1 = 0; A) x4 + 5x² + 4 = 0; B) (x + 1)x + x3 = 0; Г) x² - 2x + 1 = 0. 2
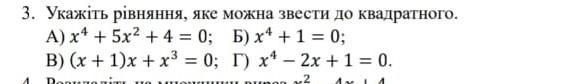
Ответы
A) Уравнение x^4 + 5x^2 + 4 = 0:
Это уравнение является квадратным по переменной x^2. Обозначим x^2 = t, тогда уравнение примет вид t^2 + 5t + 4 = 0. Мы можем решить это уравнение как квадратное уравнение относительно t, а затем найти значения x из полученных значений t.
B) Уравнение (x + 1)x + x^3 = 0:
Это уравнение не является квадратным и содержит кубическую степень переменной x. Оно не может быть приведено к квадратному виду.
Г) Уравнение x^2 - 2x + 1 = 0:
Это уравнение уже является квадратным, так как имеет вид ax^2 + bx + c = 0, где a = 1, b = -2, c = 1.
Таким образом, решением квадратного уравнения Г) будет:
x = (2 ± √(2^2 - 4 * 1 * 1)) / (2 * 1)
x = (2 ± √(4 - 4)) / 2
x = (2 ± 0) / 2
x = 1
Итак, только уравнение Г) x^2 - 2x + 1 = 0 можно привести к квадратному виду.