Question

Основанием прямой призмы является диагональ с длинами диагоналей 10 см и 24 см, а площадь боковой поверхности равна 780 см.

332. Найдите высоту длины призмы.

333. Найдите объем призмы.


Сторона основания правильной
четырехугольной призмы равна 3 корень 2
​
а диагональ призмы равна 12.

334. Найдите высоту длины призмы.

335. Найдите объем призмы.

336. Найдите градусную меру угла, образованного диагональю призмы и плоскостью основания.

337. Найдите площадь диагональной части призмы.

Answer 1

Объяснение:

№1)

Дано:

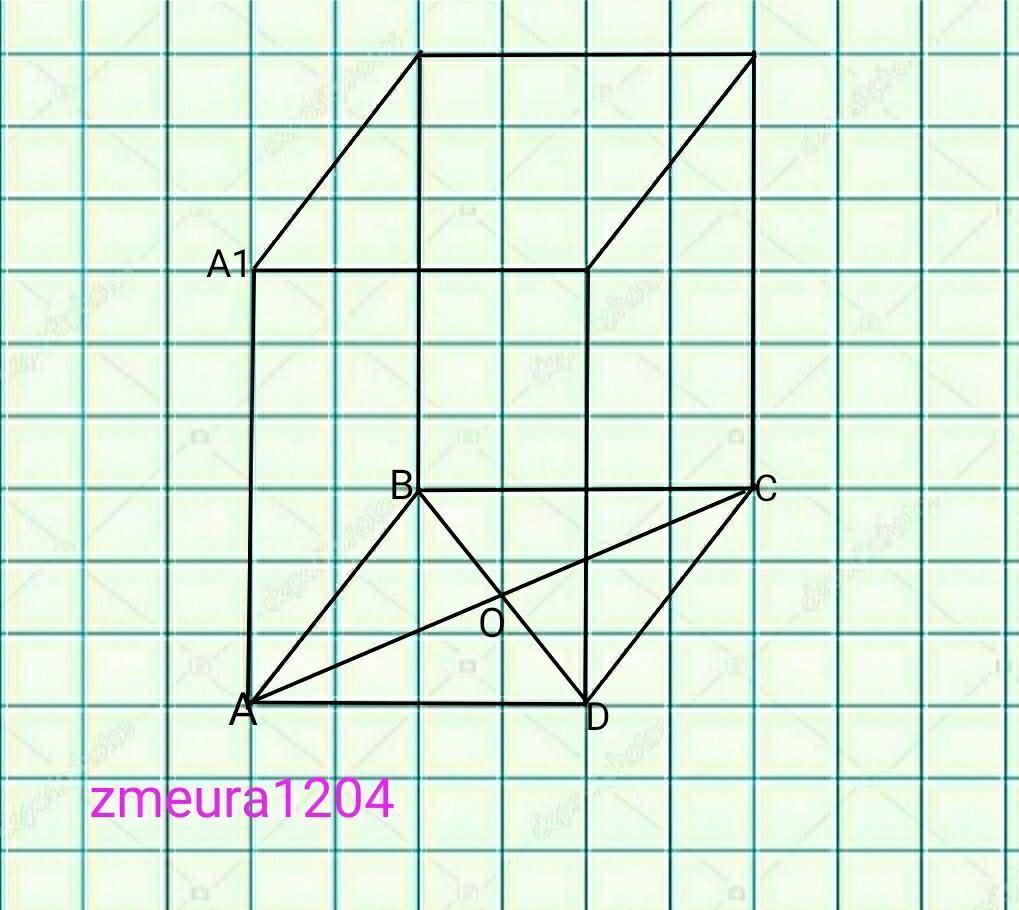
ABCDA1B1C1D1- прямая призма

ABCD - ромб

АС=24см

ВD=10см

Sб=780cм²

_______

332)

АО=ОС, свойства ромба

АО=АС/2=24/2=12см

ВО=ОD, свойства ромба

BO=BD/2=10/2=5см

∆АВО -прямоугольный треугольник

По теореме Пифагора:

АВ=√(АО²+ВО²)=√(12²+5²)=13см

Росн=4*АВ=4*13=52см

Sб=Росн*АА1; →

АА1=Sб/Росн=780/52=15см высота.

Ответ: высота призмы равна 15см

___________

333)

Sосн=½*АС*BD=½*24*10=120см²

V=Sосн*АА1=120*15=1800см³

Ответ: объем призмы равен 1800см³

###########

№2)

Дано:

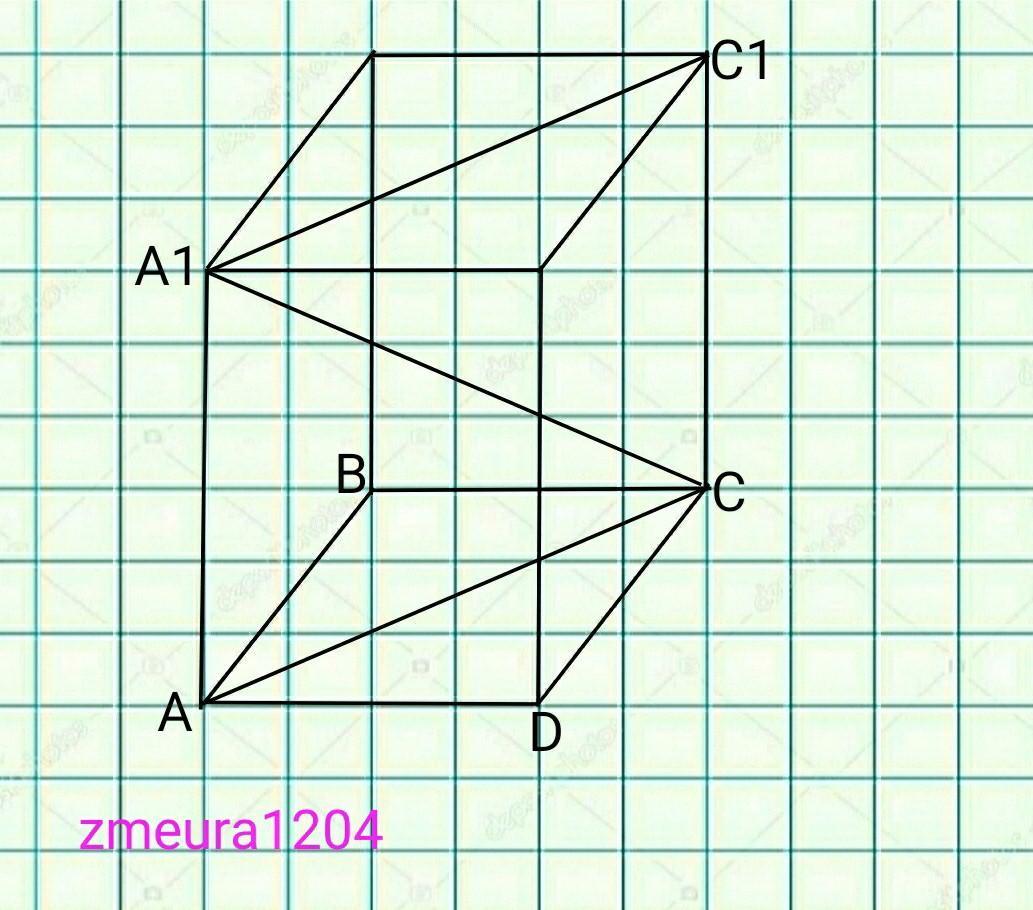
ABCDA1B1C1D1 призма

ABCD - квадрат.

АВ=3√2ед

А1С=12ед

________

334)

АС=АВ*√2=3√2*√2=6ед

∆АА1С - прямоугольный треугольник

По теореме Пифагора:

АА1=√(А1С²-АС)=√(12²-6²)=6√3ед

Ответ: высота призмы равна 6√3ед

__________

335)

Sосн=АВ²=(3√2)²=6*2=12ед.кв.

V=Sосн*АА1=12*6√3=72√3 ед.куб.

Ответ: объем призмы равен 72√3 ед³

___________

336)

АС=6см; А1С=12см

Катет АС в два раза меньше гипотенузы А1С, значит угол против которого лежит катет АС равен 30°;

∠АА1С=30°

Сумма острых углов в прямоугольном треугольнике равна 90°

∠А1СА=90°-∠АА1С=90°-30°=60° угол между диагональю и основанием

Ответ: угол между диагональю и основанием равен 60°

____________

337) ??? (если я правильно поняла перевод)

S(AA1C1C)=AA1*AC=6√3*6=36√3 ед.кв.

Ответ: площадь диагонального сечения равна 36√3 ед²