Завдання з колами, допоможіть вирішити!!!
Ответы
Відповідь:
4 см.
Пояснення:
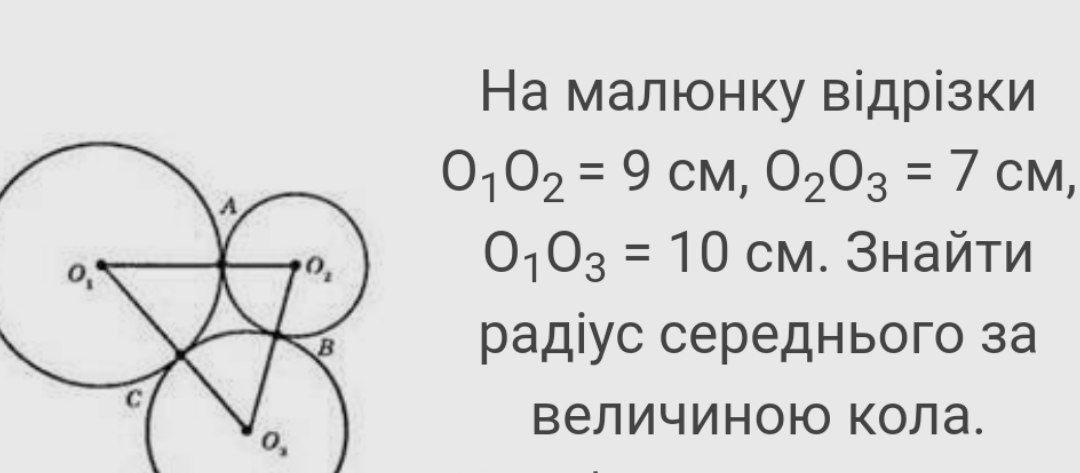
Позначимо радіус кола з центром в т.О1 - r1; радіус з центром в т.О2 - r2; радіус з центром в т.О3 - r3.
При зовнішньому дотику:
О1О2 = r1 + r2; O2O3 = r2 + r3; O1O3 = r1 + r3.
За умовою маємо:
{ r1 + r2 = 9
{ r2 + r3 = 7
{ r1 + r3 = 10
Додавши три рівняння отримаємо:
r1+r2+r2+r3+r1+r3 = 9+7+10
2r1 + 2r2 + 2r3 = 26 | :2
r1 + r2 + r3 = 13; r1 + r2 = 9,
9 + r3 = 13
r3 = 13 - 9
r3 = 4 см.
Відповідь: радіус середнього за величиною кола становить 4 см.
Відповідь:
Середнім за радіусом є коло з центром у точці О3 та радіусом R3 = 4 см.
Пояснення:
Маэмо три кола:
1) з центром у точці О1 та радіусом R1;
2) з центром у точці О2 та радіусом R2;
3) з центром у точці О3 та радіусом R3.
За умовами задачі:
О1О2 = R1 + R2 = 9 см. ( 1 )
O2O3 = R2 + R3 = 7 см. ( 2 )
O1O3 = R1 + R3 = 10 см. ( 3 )
Якщо порівняти рівняння ( 1 ) та ( 3 ), то видно, що R3 більший за R2 на 1 см. ( якщо відняти від рівняння ( 3 ) рівняння ( 1 ), отримаємо R3 - R2 = 10 - 9 = 1 см. ). Таким чином R3 = R2 + 1.
Підстановка цього виразу до рівняння ( 2 ) дає:
R2 + R2 + 1 = 7
2R2 = 7 - 1 = 6
R2 = 6 / 2 = 3 см.
R3 = 3 + 1 = 4 см.
З рівняння ( 1 ) отримаємо:
R1 + 3 = 9
R1 = 9 - 3 = 6 см.
Перевірка:
О1О2 = R1 + R2 = 6 + 3 = 9 см.
O2O3 = R2 + R3 = 3 + 4 = 7 см.
O1O3 = R1 + R3 = 6 + 4 = 10 см.
Все вірно.