Question

Найдите площадь фигуры, ограниченной графиками функций у=8/х и у= 5-0.5х

Answer 1

Ответ:  3.91   кв. ед.

Объяснение:

у=8/х;   у= 5-0.5х.

1)  Составляем таблицу значений функций при изменении аргумента

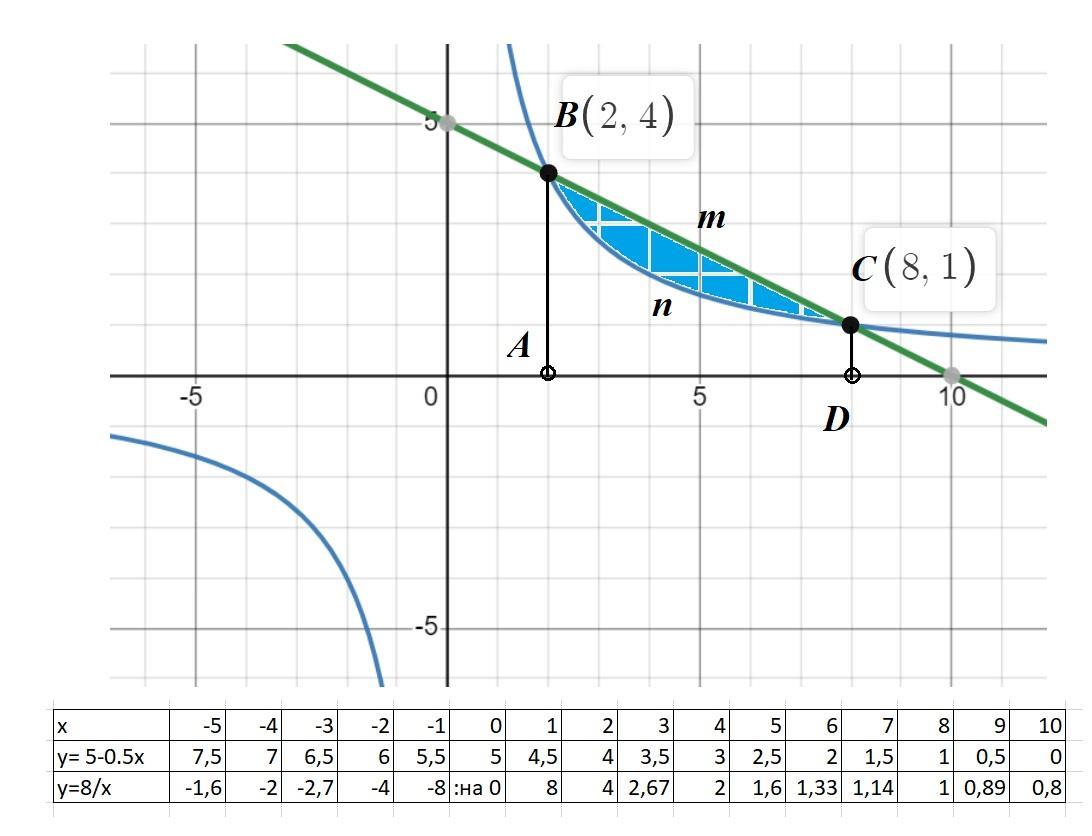
2)  Строим графики функций.  (См. скриншот).

3) Площадь находим по формуле Ньютона-Лейбница

S = S(ABmCD) - S(ABnCD) = ∫ₐᵇ(F₁(x)-F₂(x))dx = ∫ₐᵇ(F₁(x)dx - ∫ₐᵇ(F₂(x)dx =

=(F₁(x)|ₐᵇ - (F₂(x)|ₐᵇ.

4) По графику определяем пределы интегрирования (a;b) = (2;8).  Тогда

∫₂⁸(F₁(x)dx - ∫₂⁸(F₂(x)dx.

5)  F₁(x) = ∫₂⁸(5-0.5x)dx.

F₂(x)= ∫₂⁸(8/x)dx.

6)  Находим  

a)  ∫₂⁸(5-0.5x)dx=5x|₂⁸-x²/4|₂⁸ = (40-10) - 1/4(64-4) = 30 -15=15 кв. ед.

б)  ∫₂⁸(8/x)dx = 8 ∫₂⁸(1/x)dx = 8(ln|x|₂⁸) = 8(ln|8| - ln|2|) = 16*ln|2|=11.09 кв. ед.

7) Тогда  ∫₂⁸(5-0.5x)dx - ∫₂⁸(8/x)dx = 15 - 11.09 = 3.91   кв. ед.