Question

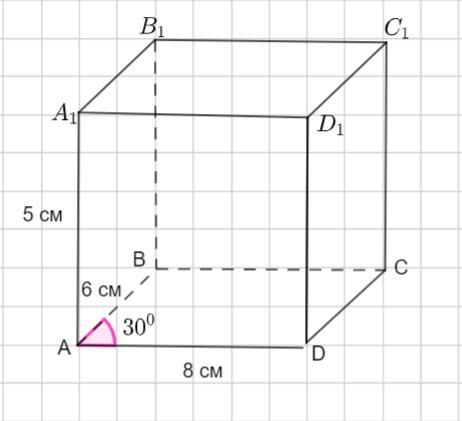
У прямому паралелепіпеді сторони основи 6 см і 8 см, кут між ними 30 градусів. Бічне ребро дорівнює 5 см. Знайти повну поверхню паралелепіпеда​

Answer 1

Ответ:

188 cм².

Объяснение:

В прямом параллелепипеде стороны основания 6 см и 8 см, а угол между ними 30 градусов. Боковое ребро равно 5 см. Найти полную поверхность параллелепипеда.

Пусть дан $ABCDA_{1} B_{1} C_{1} D_{1}$ - прямой параллелепипед

ABCD - параллелограмм со сторонами АВ = 6 см,  AD = 8 см, ∠А = 30°.

Найдем площадь полной поверхности данного параллелепипеда. Для этого надо к боковой поверхности прибавить две площади основания. Найдем площадь основания.

Площадь параллелограмма  равна произведению сторон на синус угла между ними.

$S =AD \cdot AB \cdot sin A;\\\\S =8 \cdot 6 \cdot sin 30^{0} =48\cdot \dfrac{1 }{2} =24$

Площадь параллелограмма равна 24 см ².

Площадь боковой поверхности прямого параллелепипеда равна произведению периметра основания на высоту параллелепипеда.

Периметр - это сумма длин всех сторон.

Р= 2· ( 6 + 8)= 2 · 14 = 28 см.

Боковое ребро является высотой у прямого параллелепипеда.

S = 28 · 5 = 140 cм²

Тогда полная поверхность параллелепипеда

S = 140 + 2· 24 = 140 + 48 = 188 cм².

#SPJ1