Question

Помогите по Геометрии, даю 40 баллов.
Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 8:10, считая от вершины угла при основании треугольника. Найдите стороны треугольника, если его периметр равен 52 см.

Answer 1

Ответ:

18; 18; 16.

Объяснение:

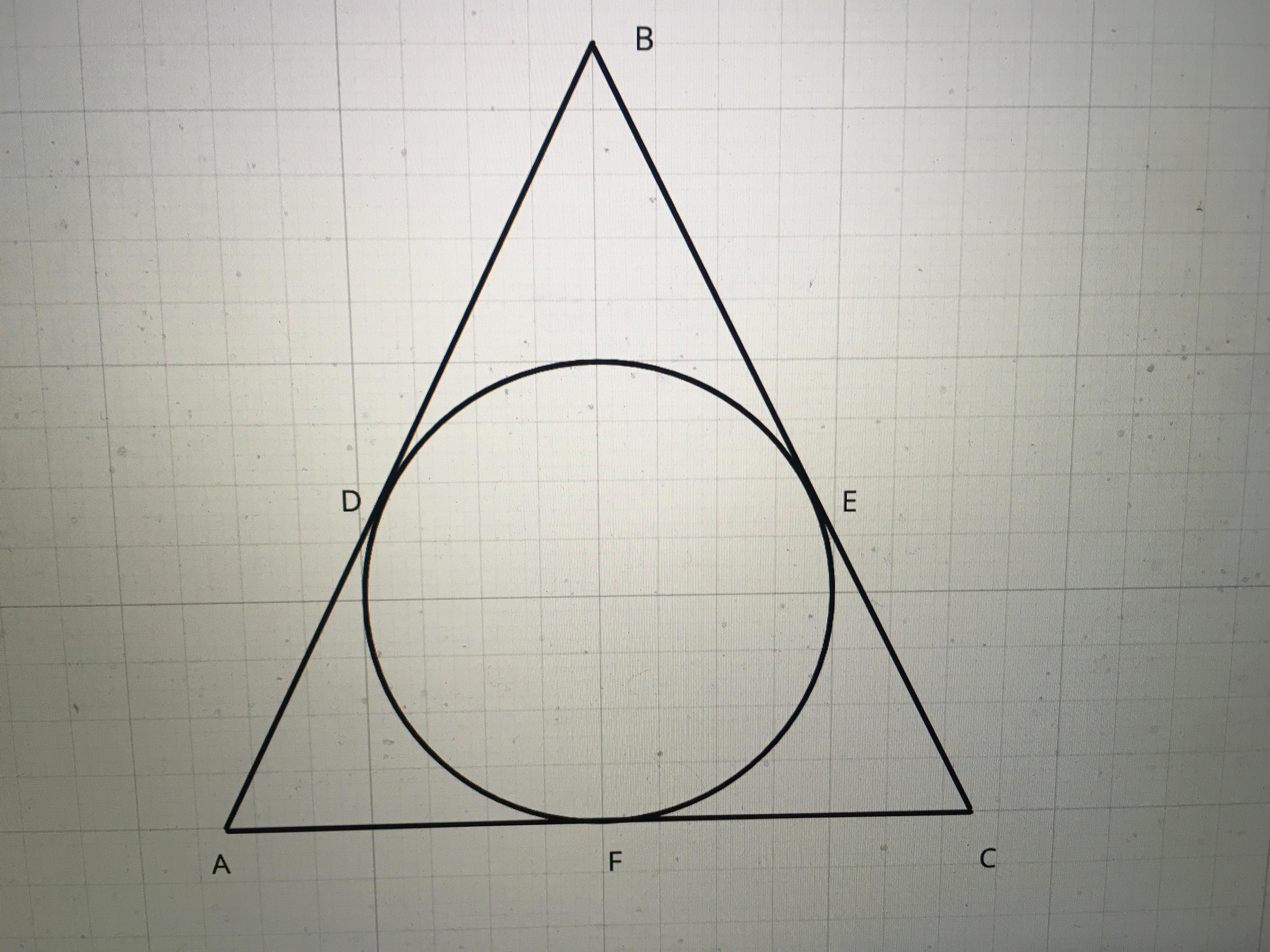
Дан треугольник ABC, AB=BC; D, E, F - точки касания вписанной окружности со сторонами AB, BC, AC соответственно. По условию AD=8t, BD=10t, а поскольку отрезки касательных AD и AF равны (как и BD=BE, CE=CF), то AD=8t, BE=10t, CE=CB-BE=AB-BD=8t, CF=CE=8t, а поскольку периметр треугольника равен 52, мы можем найти t:

              P=AB+BC+AC=8t+10t+10t+8t+8t+8t=52; 52t=52; t=1⇒

                      AB=8t+10t=18t=18; BC=AB=18; AC=8t+8t=16t=16.