Question

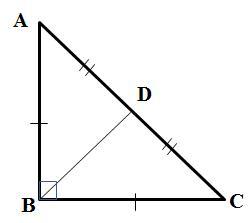
У трикутнику АВС АВ=ВС, ВD - медіана, ∠АВС = 90°. Доведіть, що Δ ВDС - рівнобедрений

Answer 1

Ответ и Пошаговое объяснение:

Перевод: В треугольнике АВС АВ = ВС, ВD – медиана, ∠АВС = 90°. Докажите, что ΔВDС – равнобедренный.

Информация: 1) Медиана треугольника — это отрезок в треугольнике, соединяющий вершину треугольника с серединой противоположной стороны.

2) В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.

Доказательство. По условию ∠АВС = 90°, то есть треугольник АВС прямоугольный (см. рисунок). Тогда медиана равна половине гипотенузы AC:

$\tt BD=\dfrac{AC}{2}.$

С другой стороны, по определению медианы

$\tt \dfrac{AC}{2}=AD=CD.$

Тогда

$\tt BD=\dfrac{AC}{2}=CD.$

Последнее равенство, то есть BD = CD означает, что ΔВDС – равнобедренный,

что и требовалось.

#SPJ1