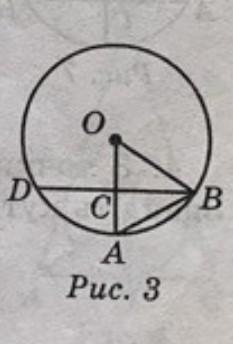
Дано: коло (0; R). BC = CD; <OBC = 20° (рис. 3). Знайдіть кути трикутника ABC.
Ответы
Ответ:
Для розв'язання цієї задачі використаємо властивість, що кут, стоячий на дуговому промені, дорівнює половині кута, що відповідає цьому дуговому променю.
Оскільки BC = CD, то <BAC = 60° (так як трикутник ABC рівнобедрений). Тоді кут BOA, що відповідає дузі BC, дорівнює 120°.
Оскільки <OBC = 20°, то <OBA (кут між дугами BC і AC) дорівнює 40°.
Також за властивістю кола, <BCA = <CDA (кути, що відповідають дузам BC і CD відповідно). Оскільки трикутник ABC рівнобедрений, то <BAC = <BCA. Тому, <BCA = <CDA = (180° - <BAC) / 2 = (180° - 60°) / 2 = 60°/2 = 30°.
Таким чином, кути трикутника ABC мають наступні значення:
<ABC = <ACB = 180° - <BAC - <BCA = 180° - 60° - 30° = 90°
<ACB = <BCA = 30°
<ABO = <OBA = 40°
Відповідь: <ABC = <ACB = 90°, <BCA = 30°, <ABO = <OBA = 40°.