Question

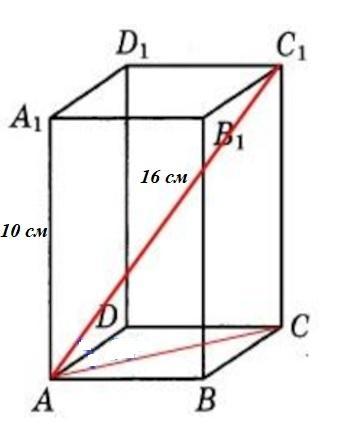
Найти V правильной четырехугольной призмы, с высотой 10 и диагональю 16.
Срочно!

Answer 1

Ответ:     780 см³.

Объяснение:

V правильной четырехугольной призмы ABCDA1B1C1D1  равен произведению трёх его измерений

V=abh = s осн.*h.

AA1=h=10 см

AC1=16 см - диагональ

-----------

Диагональ основания

AC=√(AC1²-СС1²)=√(16²-10²) = √(256-100)=√156 =2√39 см

Так как в основании призмы лежит квадрат, то

AC²= a²+a²=2a²;

2a²=156;

s осн.= a²=78 см².

Объем V=78*10 = 780 см³.