Question

Помогите пожалуйста решить задачу, физика ​

Answer 1

Ответ:

Объяснение:.....

Answer 2

Ответ:

См. решение

Объяснение:

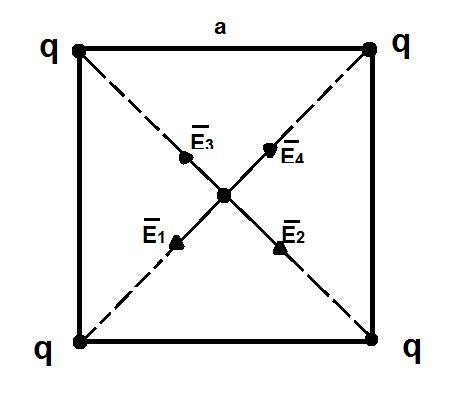
a) В силу равенства зарядов: E₁=E₂=E₃=E₄

Результирующий вектор Е есть векторная сумма напряжённостей, то есть 0( равные по модулю E₁ и E₄ лежат на одной прямой и противоположно направлены, аналогично с E₂ и E₃)

б) φ=φ₁+φ₂+φ₃+φ₄ , то есть

$\frac{4kq}{\frac{\sqrt{2}a }{2} } =\frac{8kq}{\sqrt{2} a}=\frac{8*9*10^{9}*10^{-9} }{0,2*\sqrt{2} } =254,6 B$ (Точка равноудалена от вершин, где находятся одинаковые положительные заряды, поэтому потенциалы будут равны между собой, а расстояние от заряда есть половина диаметра)

в) Можно расставить силы для любого заряда не вершине, поскольку будет всё симметрично(рисунок не приложу, потому что я не дочитал условие, когда делал первый, а ещё мне лень, в таком случае просто представляем картинку: допустим расставим силы на верхний левый заряд, на него действует сила вверх и такая же по модулю сила влево, их результирующая направлена на северо-запад, лежит на одной прямой с диагональю квадрата, а также силы со стороны центрального и нижнего правого заряда, направленные противоположно, лежащие на той же прямой). Запишем условие равновесия-векторная сумма сил равна нулю. Также осознаём факт, что разноименные заряды притягиваются, а одноимённые отталкиваются, поэтому в центре может располагаться только отрицательный заряд.

Итак

$\frac{kq^{2} \sqrt{2} }{a^{2} } =-\frac{kq^{2} }{2a^{2} }+\frac{2kq_{0}q }{a^{2} }$ (Первую силу нашёл по Пифагору, а ещё здесь q₀ взят по модулю, так бы минус тоже стоял)

Осталось решить уравнение, и если я нигде не ошибся, то даже должен получиться правильный ответ:)

$q\sqrt{2} =-\frac{q}{2}+2q_{0}\\ q_{0} =\frac{(\frac{1}{2}+\sqrt{2})q }{2} =0,96*10^{-9}$(Это модуль. Сам заряд, как я говорил, отрицательный, то есть q₀=-0,96*10⁻⁹ Кл )

На этом решение всё.