Помогите пожалуйста,срочно!! Кто решит, отдельное вам место в раю!! :
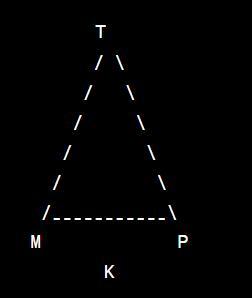
Окружность вписана в ∠MKP, M и P - точки касания прямых KP и KM и окружности. Точка T лежит на окружности так,что ∠MTP = 20°. Найдите величину угла MKP.
(нужен рисунок ещё)
Ответы
Ответ:
Накалякал чертеж как мог в приложении.. (чертеж в фото)
Объяснение:
Для решения задачи мы воспользуемся свойством: угол, образованный хордой и касательной, равен половине соответствующего центрального угла.
Пусть O - центр вписанной окружности, тогда ∠OMT = 90°, так как OT является радиусом окружности. Также заметим, что ∠MTO = ∠MTP = 20°, так как точка T лежит на окружности.
Таким образом, имеем:
∠OMK = ∠OMP = 90°/2 = 45° (так как MK и MP являются касательными)
∠MOK = 180° - ∠OMK - ∠OMP = 180° - 45° - 45° = 90° (сумма углов в треугольнике MOK равна 180°)
Теперь рассмотрим треугольник MTK:
∠MKT = ∠MTK = (180° - ∠MTO)/2 = (180° - 20°)/2 = 80°
∠KMT = 180° - ∠MKT - ∠MKT = 180° - 80° - 80° = 20°
Наконец, рассмотрим треугольник MKP:
∠MKP = ∠MKT + ∠KPT = 80° + 90° = 170° (так как KT является радиусом окружности)
Таким образом, величина угла MKP равна 170°.