Предмет: Алгебра,
автор: besenyjbober32
помогите плиз скоро надо сдавать..
Докажите тождество
Приложения:
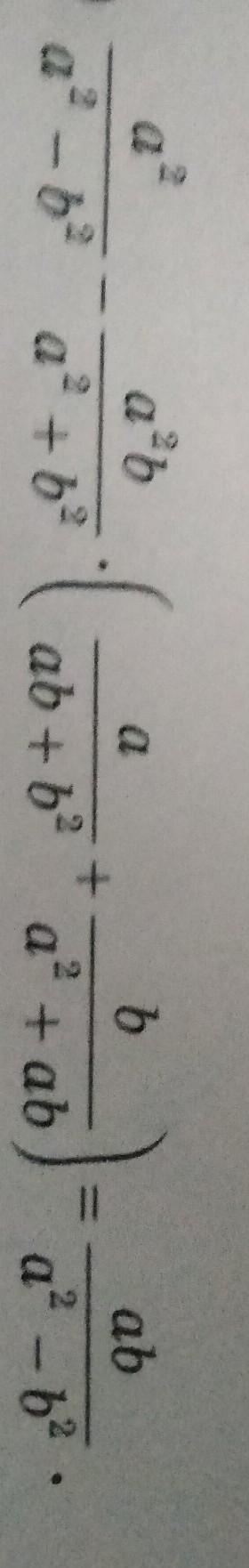
Ответы
Автор ответа:
1
Тождество доказано
besenyjbober32:
пасибки
Похожие вопросы
Предмет: Українська література,
автор: asuragol13
Предмет: Математика,
автор: thebatya7
Предмет: География,
автор: Andrey1266664
Предмет: Алгебра,
автор: yanabannikova2005
Предмет: Алгебра,
автор: Аноним