Нужно решить системы дифференциальные уравнений !!!!!! СРОЧНО ПЖППЭПЖЭПЖП
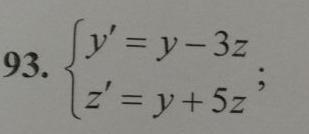
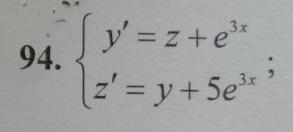
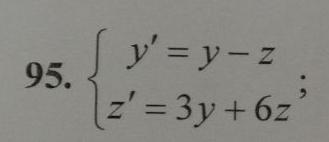
Ответы
Ответ:
1)
Дана система диференціальних рівнянь:
y' = y - 3z
z' = y + 5z
Для знаходження загального розв'язку системи можна скористатися методом елімінації невідомих. Для цього необхідно спочатку знайти значення однієї з невідомих, наприклад, z, через іншу невідому y, і підставити це значення в друге рівняння системи для знаходження y.
З першого рівняння системи можна виділити змінну z:
z = (y - y')/3
Підставимо це значення змінної z в друге рівняння системи:
y' = y - 3((y - y')/3) + 5y
y' = 2y - y'
2y = 2y'
y = y'
Отже, отримали, що y = y'. Підставимо це значення в формулу для змінної z:
z = (y - y')/3 = 0
Отже, з = 0. Тепер можна записати загальний розв'язок системи:
y(t) = C1e^t
z(t) = 0
де С1 - будь-яка константа.
Таким чином, достовірною є тільки змінна y, а змінна z залишається постійною і дорівнює нулю.
2) Дана система диференціальних рівнянь:
y' = z + e^(3x)
z' = y + 5e^(3x)
Щоб знайти загальний розв'язок цієї системи, можна використовувати метод інтегрування за частинами.
З першого рівняння можна знайти залежність z від x:
z = y' - e^(3x)
Підставивши це значення в друге рівняння, отримаємо нове рівняння, залежне лише від y та x:
y'' - 3y' - 5e^(3x) = 0
Щоб знайти загальний розв'язок цього рівняння, можна використати характеристичний рівняння:
λ^2 - 3λ - 5e^(3x) = 0
Корені цього рівняння можна знайти за допомогою формули коренів квадратного рівняння:
λ = (3 ± sqrt(9 + 20e^(3x))) / 2
Таким чином, загальний розв'язок для y має вигляд:
y(x) = c1 * e^((3 + sqrt(9 + 20e^(3x))) / 2 * x) + c2 * e^((3 - sqrt(9 + 20e^(3x))) / 2 * x) + 5/20 * e^(3x)
де c1 та c2 - довільні константи.
Знаючи залежність z від y, можна виразити z залежно від x:
z = y' - e^(3x) = (c1/2) * sqrt(9 + 20e^(3x)) * e^((3 + sqrt(9 + 20e^(3x))) / 2 * x) - (c2/2) * sqrt(9 + 20e^(3x)) * e^((3 - sqrt(9 + 20e^(3x))) / 2 * x) + (15/20) * e^(3x) - e^(3x)
Отже, загальний розв'язок системи має вигляд:
y(x) = c1 * e^((3 + sqrt(9 + 20e^(3x))) / 2 * x) + c2 * e^((3 - sqrt(9 + 20e^(3x))) / 2 * x) + 5/20 * e^(3x)
z(x) = (c1/2) * sqrt(9 + 20e^(3x)) * e^((3 + sqrt(9 + 20e^(3x))) / 2 * x) - (c2/2) * sqrt(9 + 20e^(3x)) * e^((3 - sqrt(9 + 20e^(3x))) / 2 *
\
3)Ця система диференціальних рівнянь має вигляд:
y' = y - z
z' = 3y - 6z
Для розв'язання системи використаємо метод елімінації невідомих. Спочатку відновимо попередні вирази для y та z з першого та другого рівняння відповідно:
y = y' + z
z = (3y - z) / 6 = y/2 - z/2
Підставляємо вираз для y у друге рівняння:
z' = 3(y' + z) - 6z
Після спрощення отримаємо:
z' = 3y' + 3z - 3z
z' = 3y'
Отже, маємо два рівняння:
y' = y - z
z' = 3y'
З першого рівняння виразимо z:
z = y - y'
Підставимо цей вираз у друге рівняння:
(y - y')' = 3y'
y' - y'' = 3y'
y'' + 2y' - y = 0
Розв'язуємо характеристичне рівняння:
r^2 + 2r - 1 = 0
Отримуємо два корені:
r1 = -1 - sqrt(2)
r2 = -1 + sqrt(2)
Тоді загальний розв'язок має вигляд:
y = c1 * e^(r1 * t) + c2 * e^(r2 * t) + 2 * t
де c1 та c2 - довільні константи, що залежать від початкових умов.
Підставляємо отримане значення y у вираз для z:
z = y - y' = c1 * e^(r1 * t) + c2 * e^(r2 * t) + 2 * t - (c1 * r1 * e^(r1 * t) + c2 * r2 * e^(r2 * t))
Таким чином, ми знайшли загальний розв'язок системи диференціальних рівнянь.