Question

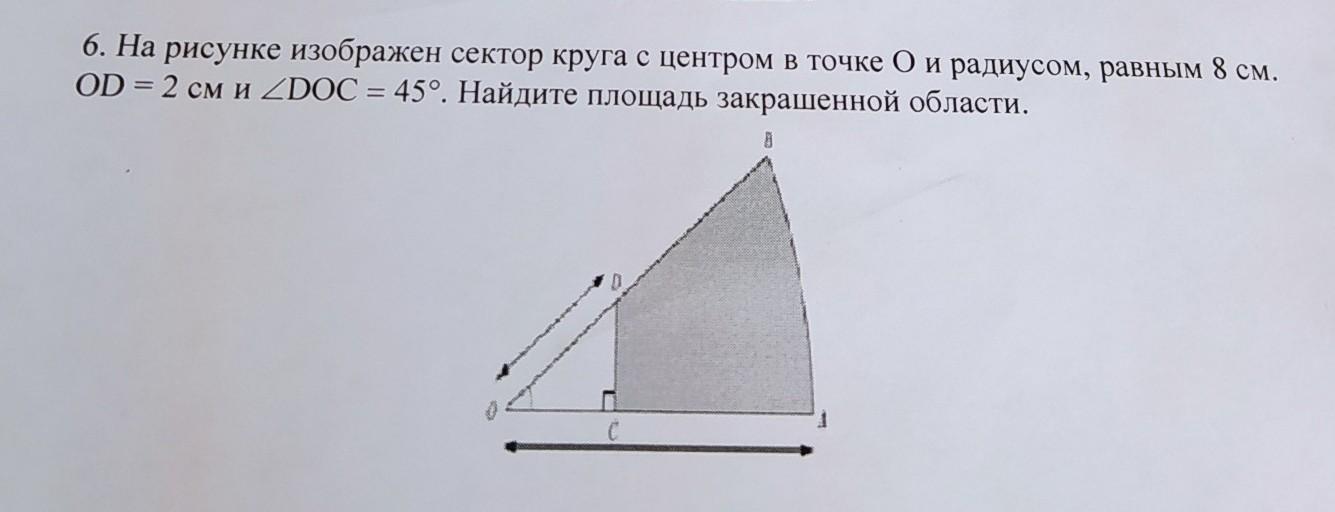
6. На рисунке изображен сектор круга с центром в точке О и радиусом, равным 8 см. OD = 2 см и уголDOC = 45°. Найдите площадь закрашенной области.​

Answer 1

Ответ:   24.14 см².

Объяснение:

S(OAB) = πR²∠(DOC)/360° = π*8²*45°/360° = 8π см²;

OC/OD = cos45°;

OC=OD*cos45° =2*√2/2 = √2=1.41 см;

S(OCD) = 1/2OC*CD=>  так как ΔOCD-равнобедренный, то

OC=CD=1,41 см.

S(OCD) = 1/2*1.41² = 0.994 см^2.

S(ABDC)=S(OAB)-S(OCD) = 8π-0.994=24.14 см².