Question

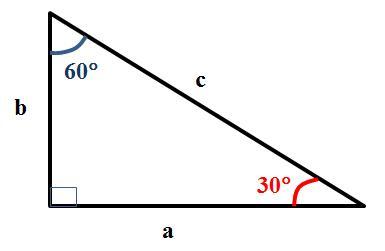
В прямоугольном треугольнике один из углов равен 30°, а разность гипотенузы и меньшего из катетов равна 17.
Чему равен меньший катет?
Чему равна гипотенуза?

Answer 1

Ответ:

Меньший катет равен 17, а гипотенуза равна 34

Объяснение:

Информация: 1) Напротив меньшей стороны треугольника лежит меньший угол, а напротив меньшего угла меньшая сторона.

2) Сумма острых углов прямоугольного треугольника равна 90º.

3) В прямоугольном треугольнике катет, лежащий напротив угла 30°, равен половине гипотенузы.

Решение. Пусть в прямоугольном треугольнике гипотенуза c, а напротив угла 30° лежит катет b (см. рисунок). Значит, другой острый угол прямоугольного треугольника равен 90º-30º = 60º. По свойству, приведённой выше, меньший катет - это b.

По условию c – b = 17 (первое уравнение). Катет b лежит напротив угла 30° в прямоугольном треугольнике и поэтому c = 2·b (второе уравнение). Второе уравнение подставим в первое уравнение и находим меньший катет b:

2·b – b = 17 или b = 17.

Теперь определим длину гипотенузы:

c = 2·17 = 34.

#SPJ1