Решите задачу, с рисунком

Ответы
Ответ:
Боковая поверхность правильной четырехугольной пирамиды равна 8√2 см².
Объяснение:
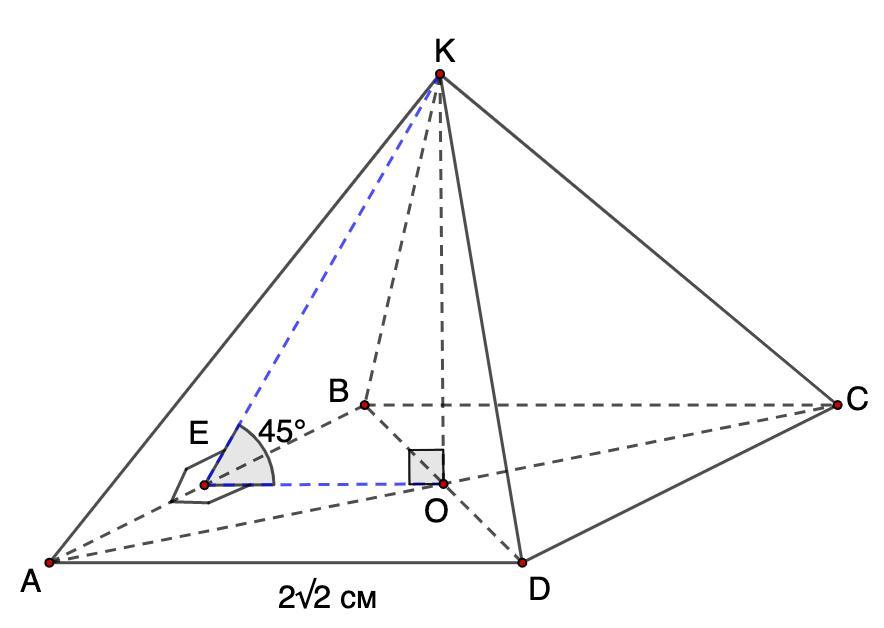
Найдите боковую поверхность правильной четырехугольной пирамиды, если сторона основания равна 2√2 см, а все двугранные углы при основании - 45°.
Дано: KABCD - правильная четырехугольная пирамида.
АВ = 2√2 см;
Двугранный угол при основании равен 45°.
Найти: S бок.
Решение:
- В правильной четырехугольной пирамиде в основании лежит квадрат, а все боковые грани - равнобедренные треугольники.
Определим двугранный угол.
- Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости.
⇒ КАВО - двугранный угол.
Двугранный угол измеряется его линейным углом.
- Линейным углом двугранного угла называется угол, полученный в результате пересечения данного двугранного угла и какой- нибудь плоскости, перпендикулярной его ребру а.
Проведем КЕ ⊥ АВ.
ЕО - проекция КЕ на (АВС)
- Если на плоскости через основание наклонной проведена прямая, перпендикулярная ей самой, то она перпендикулярна и ее проекции.
⇒ ОЕ ⊥ АВ.
∠КЕО = 45° - линейный угол двугранного угла.
Рассмотрим ΔЕКО - прямоугольный.
ЕО = AD : 2 = 2√2 : 2 = √2 (см) (ABCD - квадрат)
∠КЕО = 45°
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠ЕКО = 90° - ∠КЕО = 90° - 45° = 45°
- Если в треугольнике два угла равны, то он равнобедренный.
⇒ ОЕ = ОК = √2 (см)
По теореме Пифагора найдем КЕ:
КЕ² = ЕО² + ОК² = 4 ⇒ КЕ = 2 см
- Площадь боковой поверхности правильно пирамиды равна:
S бок. = 1/2 · Р осн. · l ,
где l - апофема.
P(ABCD) = 2√2 · 4 = 8√2√ (см)
S бок. = 1/2 · 8√2 · 2 = 8√2 (см²)
#SPJ1