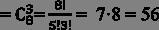У ящику 8 білих і 6 чорних кульок. Вибираємо навмання 3 з них. Яка ймовірність того, що:
1) всі 3 кульки білі
2) дві кульки білі та 1 чорна
3) серед кульок є як і білі, так і чорні?
Ответы
Ответ:
Пошаговое объяснение:
Розвязання 1. Загальна кількість способів вибрати три кульки з 8+6=14 кульок дорівнює n=C3/14=14!/11!3!=2*13*14=364. Вибрати три білі кульки з 8 дорівнює m=C3/8=8!/5!3!=7*8=56. - кількість сприятливих подій.
Отже,p(A) = m/n = 7*8/2*13*14 =2/13.
Відповідь:p(A) = 2/13.
2. Вибрати 2 білі кульки з 8 дорівнює C2/8=8!/6!2!=4*7=28, а вибрати одну чорну кульку з шести дорівнює C1/6=6. За правилом добутку загальна кількість сприятливих подій дорівнює m=C2/8*C1/6=28*6=168.
Отже, p(A) =m/n=4*7*6/2*13*14=6/13.
3. Якщо чорних кульок дві, а былих - одна,а кількість способів їч вибрати дорівнює m1=C2/8*C1/6=28*6=168.Якщо білих кульок дві, а чорних - одна,а кількість способів їч вибрати дорівнює m2=С1/8*C2/6=8*15=120. За правилом суми загальна кількість сприятливих подій дорівнює m=m1+m2=168+120=288.
Отже,p(A) = m/n= 288/364=72/91.
Відповідь: p(A) =72/91.
(прикріпила фото як правильно писати розв'язки, будь-ласка відмітіть як краща відповідь)