Предмет: Алгебра,
автор: rtyggree
решите АЖПЖПЖПЖПЖ8 < x ^ 2 - 4x + 3 <= 15
Приложения:
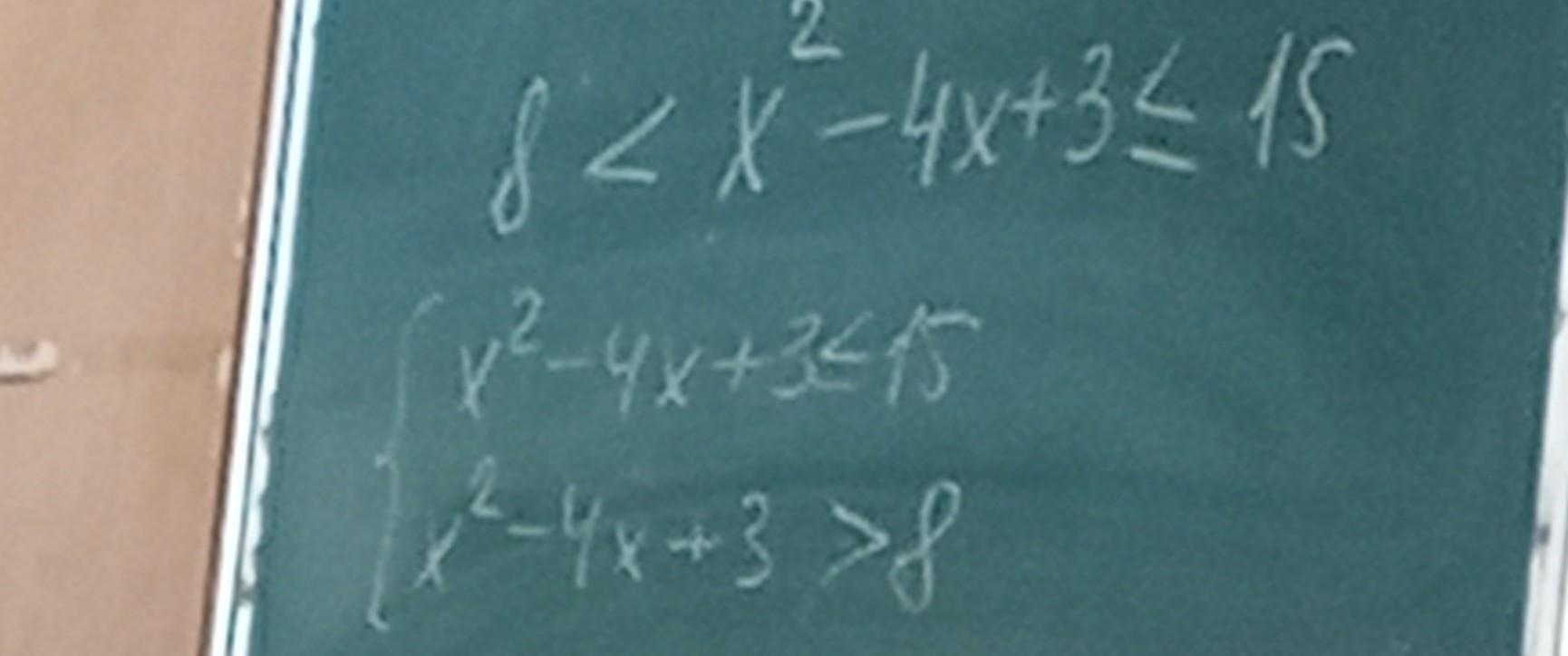
Ответы
Автор ответа:
1
Объяснение:
-∞__+__-1__-__5__+__+∞
x∈(-∞;-1)U(5;+∞).
-∞__+__-2__-__6__+__+∞
x∈[-2;6]. ⇒
Ответ: x∈[-2;-1)U(5;6].
Похожие вопросы
Предмет: Английский язык,
автор: dididid49
Предмет: Физика,
автор: ernar2010022
Предмет: Алгебра,
автор: Laespada
Предмет: Українська мова,
автор: yourxkami
Предмет: Английский язык,
автор: hfcfggvAlexyabd2008