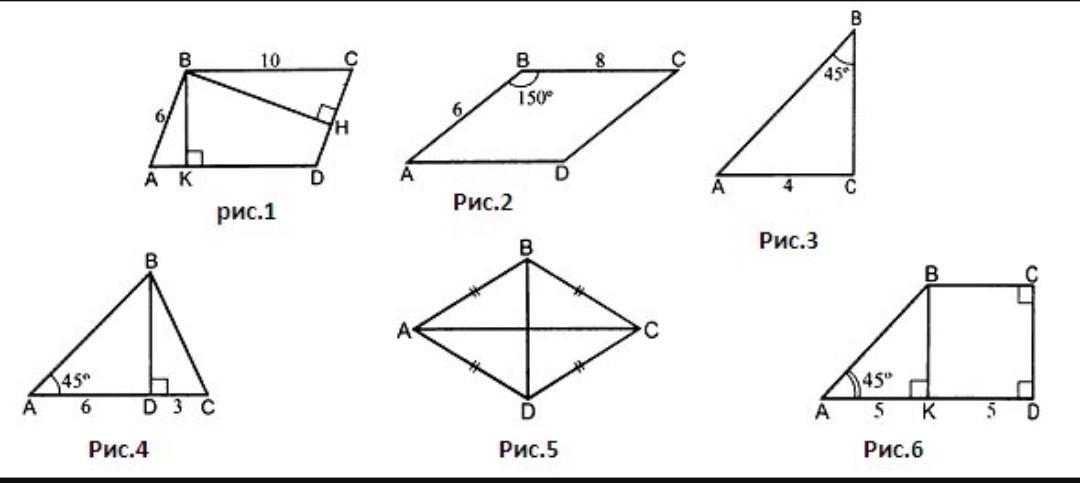
Рис. 1. ABCD – параллелограмм, BH = 8 см. Найти ВК. 2. Рис. 2. ABCD – параллелограмм. Найти SABCD 3. Рис. 3. Найти SABC 4. Рис. 4. Найти SABC 5. Рис. 5. АС = 12, SABCD = 48. Найти BD. 6. Рис. 6. Найти SABCD
Ответы
1. Так как BH является высотой параллелограмма, то VK = BH = 8 см.
2. Площадь параллелограмма равна произведению длины одной стороны на высоту, опущенную на эту сторону. Так как высота равна BH, а длина стороны AB равна CD, то SABCD = AB * BH = CD * BH.
3. Площадь треугольника равна половине произведения длины основания на высоту, опущенную на это основание. Так как основание равно AB, а высота равна BH, то SABC = (AB * BH) / 2.
4. Так как треугольник SAB является прямоугольным, то его площадь равна половине произведения катетов. Так как катеты равны SA и AB, то SABC = (SA * AB) / 2.
5. Так как площадь параллелограмма равна произведению длины одной стороны на высоту, опущенную на эту сторону, то AB * BH = 48. Так как AB = CD, то CD * BH = 48. Таким образом, мы имеем систему уравнений:
AB * BH = 48
CD * BH = 48
Из первого уравнения получаем AB = 48 / BH = 6 см. Из второго уравнения получаем CD = 6 см. Так как BD является диагональю параллелограмма, то он делит его на два равных треугольника. Таким образом, треугольник ABD является прямоугольным, и мы можем применить теорему Пифагора:
BD^2 = AB^2 + AD^2
Так как AD равно высоте параллелограмма, опущенной на сторону AB, то AD = BH = 8 см. Подставляем известные значения и получаем:
BD^2 = 6^2 + 8^2
BD^2 = 100
BD = 10 см.
6. Так как площадь параллелограмма равна произведению длины одной стороны на высоту, опущенную на эту сторону, то AB * BH = SABCD. Так как AB = CD, то CD * BH = SABCD. Таким образом, мы имеем систему уравнений:
AB * BH = SABCD
CD * BH = SABCD
Из первого уравнения получаем AB = SABCD / BH. Из второго уравнения получаем CD = SABCD / BH. Так как параллелограмм ABCD разбивается диагональю на два равных треугольника, то площадь каждого из них равна половине площади параллелограмма. Таким образом, мы можем выразить SABCD через стороны треугольника SAB:
SABCD = 2 * SABC = 2 * ((SA * AB) / 2) = SA * AB
Подставляем известные значения и получаем:
SABCD = 12 * AB
SABCD = 12 * CD
SABCD = 12 * (SABCD / BH)
Решаем уравнение относительно SABCD:
SABCD = 12 * (SABCD / BH)
SABCD * BH = 12 * SABCD
BH = 12
Таким образом, SABCD = AB * BH = CD * BH = 6 * 12 = 72 см^2.