Предмет: Математика,
автор: panteraya2005
Знайти асимптоми графіка функції!!
Приложения:
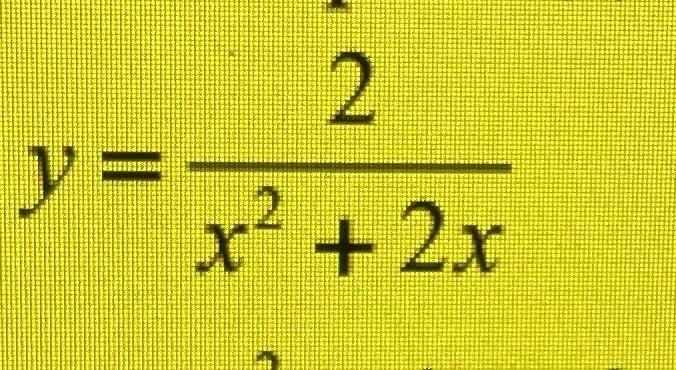
Ответы
Автор ответа:
1
Ответ:
Вертикальными асимптотами будут прямые х=0 и х= -2 .
Действительно ,
Наклонную асимптоту ищем в виде .
Уравнение асимптоты имеет вид : (ось ОХ) . Это горизонтальная асимптота , частный случай наклонной асимптоты .
Приложения:

Похожие вопросы
Предмет: Українська література,
автор: robottttt7
Предмет: Английский язык,
автор: vladpech2007
Предмет: Английский язык,
автор: karimovamumtoza54
Предмет: Английский язык,
автор: timofei430
Предмет: Математика,
автор: Olga270983