Предмет: Алгебра,
автор: SsInostrankasS
Помогите пожалуйста,очень срочнооо;;
Тема: похідна складеної функції
Приложения:

Ответы
Автор ответа:
0
Ответ:
Производная сложной функции .
Формула : .
Формула : .
Приложения:
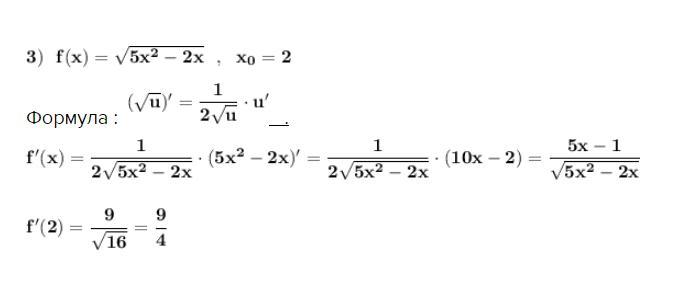
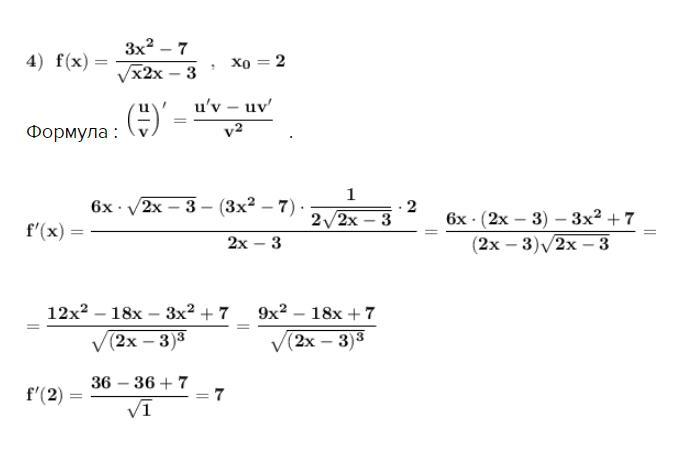
SsInostrankasS:
Просто вижу,что вы написали "Производная сложной функции" и думаю,что переводчик возможно не правильно перевёл и там сложенная,подходит ли это решение под тему : производная сложенной функции? Просто смотрела разбор и там нужно поочереди делать и тд, что-то вообще запуталась теперь
Похожие вопросы
Предмет: Химия,
автор: sklarskijdana873
Предмет: Математика,
автор: sasha20122201
Предмет: Химия,
автор: skillsf302
Предмет: Українська мова,
автор: lesyahanich
Предмет: История,
автор: nastyashmarina04