Предмет: Алгебра,
автор: y10460361
СРОЧНО !!!!!!!!!!!!!!!!! 100 балов даю
Приложения:
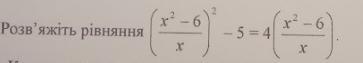
Ответы
Автор ответа:
0
Автор ответа:
1
Пусть , тогда
Возвращаем переменную и решаем 2 уравнения
Похожие вопросы
Предмет: География,
автор: alinamisiuk258
Предмет: Английский язык,
автор: vladsirica6
Предмет: История,
автор: fedorenkoartem816
Предмет: Математика,
автор: Persikhert