Предмет: Алгебра,
автор: nastabelaeva
Помогите пожалуйста!!
Приложения:
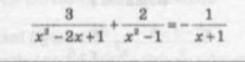
Ответы
Автор ответа:
1
Ответ:
Вот то самое пошаговое решение,думаю помогла
Приложения:



nastabelaeva:
спасибо большое:)
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: nyarar0000
Предмет: Математика,
автор: 204829929
Предмет: История,
автор: sokurenkoivan
Предмет: Информатика,
автор: diana050596
Предмет: Математика,
автор: Inna776