Вычислить площадь фигуры ограниченной параболой y=4x-x^2, y=4-x
Даю все баллы
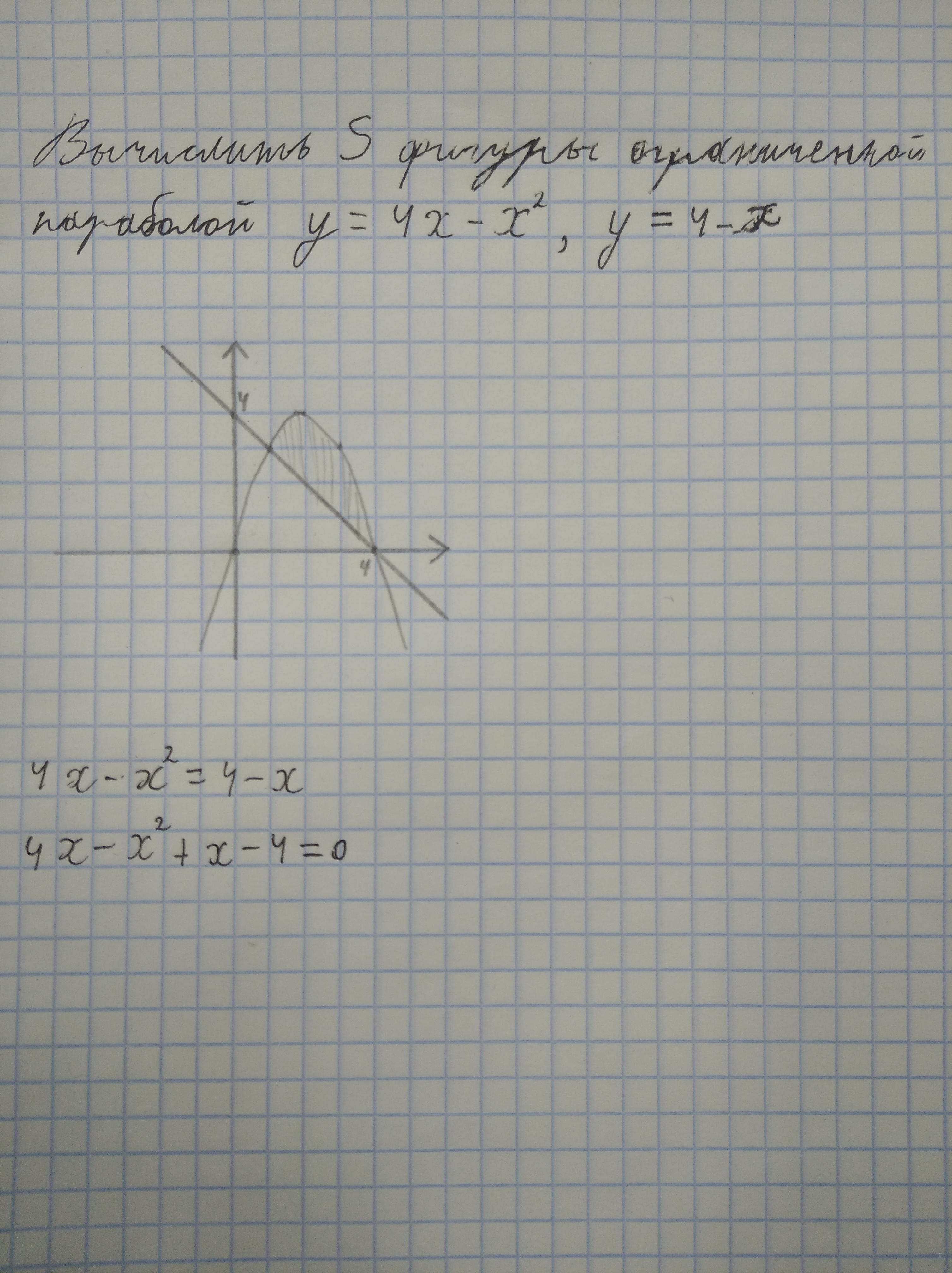
Ответы
Ответ:
Для решения задачи необходимо найти точки пересечения двух заданных кривых. Затем нужно найти интеграл функции y=4x-x^2 на интервале от x1 до x2, где x1 и x2 - это координаты точек пересечения соответствующих прямых. Формула для вычисления площади ограниченной двумя кривыми вдоль оси х имеет вид:
S = ∫(x1→x2)f(x) - g(x) dx,
где f(x) - уравнение верхней кривой, g(x) - уравнение нижней кривой.
Найти точки пересечения кривых:
4x - x^2 = 4 - x
x^2 + 3x - 4 = 0
(x + 4)(x - 1) = 0
x1 = -4, x2 = 1
Таким образом, для вычисления площади фигуры ограниченной параболой y=4x-x^2 и прямой y=4-x, необходимо посчитать следующий интеграл:
S = ∫(-4→1)(4x - x^2) - (4 - x) dx
S = ∫(-4→1)(5x - x^2 - 4) dx
S = 5/2*x^2 - 1/3*x^3 - 4x
S = (5/2*1^2 - 1/3*1^3 - 4*1) - (5/2*(-4)^2 - 1/3*(-4)^3 - 4*(-4))
S = 5/2 - 1/3 + 4 - (5*8 - 64 - 16)
S = 10/6 + 18
S = 26/3
Ответ: площадь фигуры ограниченной параболой y=4x-x^2 и прямой y=4-x равна 26/3.
Ответ:
Уравнение прямой ищем: (x-1)/(4-1)=(y-3)/(0-3)
1-x=y-3; y=4-x.
Ищем точки пересечения линий:
4x-x²=4-x; x₁=0; x₂=4
S=∫₀⁴(4x-x²-4+x)dx=∫₀⁴(-4+5x-x²)dx=(-4x+5x²/2-x³/3)|₀⁴=-16+80-64/3=...
С арифметикой справитесь?