Question

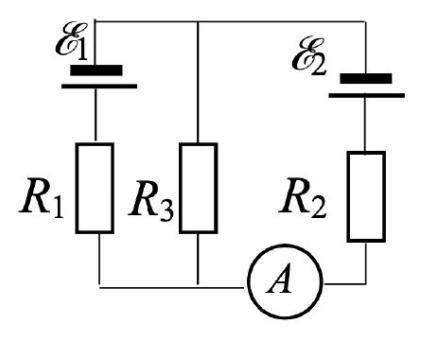
Два источника тока с ЭДС E1 = 110 В и E2 = 220 В и три резистора с сопротивлениями R1 = 100 Ом, R2 = 100 Ом и R3 = 500 Ом соединены так как показано на рисунке. Определить силы токов в трех резисторах. Внутренним сопротивлением источников питания пренебречь. (Решить данную задачу правилом Кирхгофа)

Answer 1

Ответ:

Для решения задачи методом Кирхгофа необходимо применить законы Кирхгофа:

- первый закон Кирхгофа (закон о сохранении заряда): алгебраическая сумма токов, сходящихся в узле, равна нулю;

- второй закон Кирхгофа (закон об узловых напряжениях): алгебраическая сумма произведений сопротивлений на силы тока в каждом замкнутом контуре равна алгебраической сумме падений напряжения на элементах этих контуров.

Применяя второй закон Кирхгофа, составим систему уравнений:

- для контура АВCD: E1 - I1R1 - I2R3 = 0;

- для контура ADEF: E2 - I2R2 - I1R3 = 0.

Применяя первый закон Кирхгофа, получим: I1 + I2 - I3 = 0.

Решая эту систему уравнений, найдем силы токов в каждом резисторе:

I1 = (E2R1 - E1R3) / (R1R2 + R1R3 + R2R3) = (220100 - 110500) / (100100 + 100500 + 100500) ≈ -0.22 А (ток направлен в обратную сторону);

I2 = (E1R2 - E2R3) / (R1R2 + R1R3 + R2R3) = (110100 - 220500) / (100100 + 100500 + 100500) ≈ -0.66 А (ток направлен в обратную сторону);

I3 = -I1 - I2 ≈ 0.88 А.

Следовательно, сила тока в резисторе R1 равна |I1| ≈ 0.22 А, в резисторе R2 - |I2| ≈ 0.66 А, в резисторе R3 - |I3| ≈ 0.88 А.