Question

ДАЮ 40 БАЛЛОВ СРОЧНО
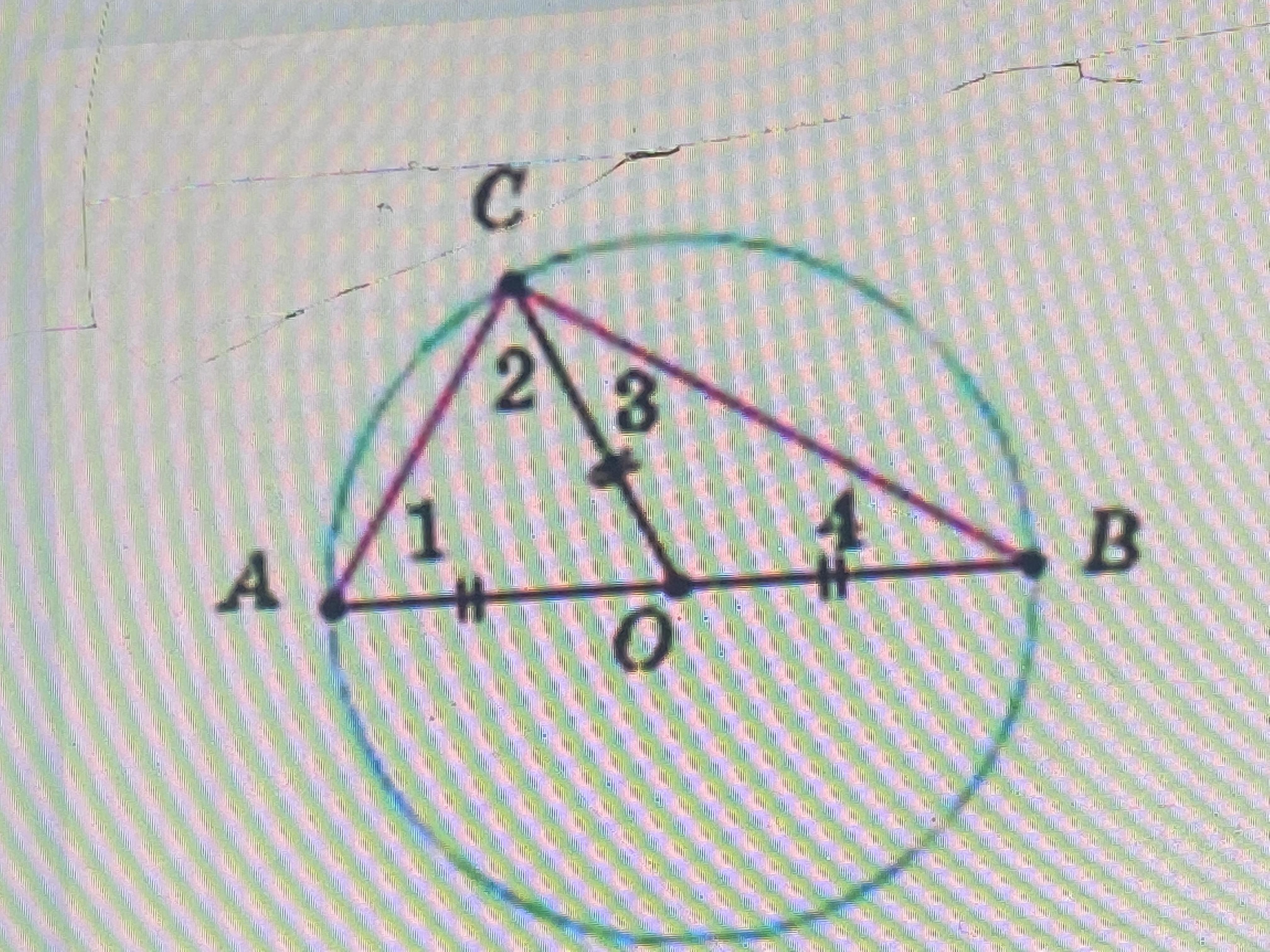
Навколо трикутника АВС описане коло з центром О. АВ-діаметр кола. Знайти кут САВ якщо ВСО 40 градусів

Answer 1

Ответ:

∠CAB = 50°

Объяснение:

Информация: 1) Вписанный в окружность угол, опирающийся на диаметр, всегда прямой.

2) В равнобедренном треугольнике углы при основании равны.

Решение. Так как OA=OB=OC - радиусы окружности, то треугольник COB равнобедренный с основанием BC и треугольник COA равнобедренный с основанием AC. Тогда

∠CBA = ∠CBO = ∠BCO = 40° и ∠CAB = ∠CAO = ∠ACO.

По условию AB диаметр и поэтому угол ACB прямой, то есть

∠ACB = 90°. Так как

∠ACO + ∠BCO = ∠ACB = 90°, то ∠ACO = 90° – ∠BCO = 90° – 40° = 50°.

Но тогда из-за равенства ∠CAB = ∠ACO получаем ∠CAB = 50°.

#SPJ1