Question

помогите пожалуйста решить задачу ​

Answer 1

Ответ:

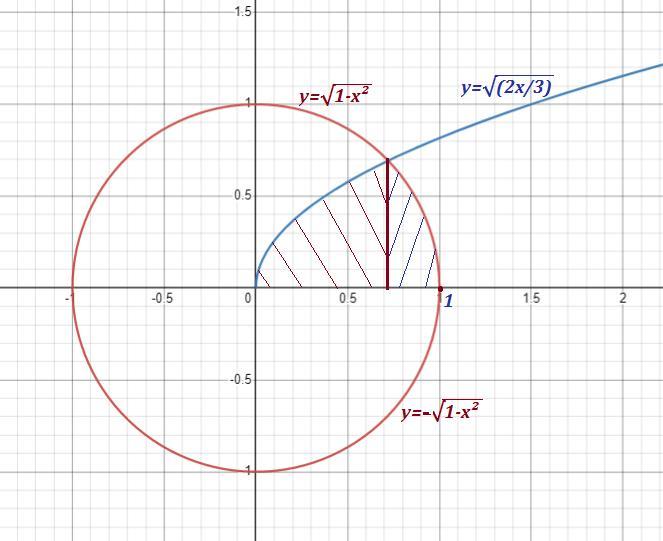
Объём тела вращения вокруг оси ОХ :  $\displaystyle \bf V_{ox}=\pi \int\limits_{a}^{b}\, y^2(x)\, dx$   .

$\bf x^2+y^2=1\ \ ,\ \ y=\sqrt{\dfrac{2x}{3}}$  

Область ограничена верхней полуокружностью и верхней ветвью параболы .

Точка пересечения :

$\bf x^2+y^2=1\ \ \ \to \ \ y^2=1-x^2\\\\y=\sqrt{\dfrac{2x}{3}}\ \ \to \ \ \ y^2=\dfrac{2x}{3}\\\\1-x^2=\dfrac{2x}{3}\ \ \ \to \ \ \ \ 3-3x^2=2x\ \ ,\ \ \ 3x^2+2x-3=0\ \ ,\\\\D/4=(b/2)^2-ac=1^2+9=10\ \ ,\ \ x_1=\dfrac{-1-\sqrt{10}}{3}\ ,\ x_2=\dfrac{-1+\sqrt{10}}{3}$

Подходит по смыслу положительное значение  $\bf x_2$  .

$\displaystyle \bf V_{ox}=\pi \int\limits_{\frac{-1+\sqrt{10}}{3} }^1\, \sqrt{\frac{2x}{3}}\, dx+\pi \int\limits_0^{\frac{-1+\sqrt{10}}{3} }\, \sqrt{1-x^2}\ dx=$  

$\bf \displaystyle =\pi \, \sqrt{\frac{2}{3}}\cdot \frac{2\sqrt{x^3}}{3}\ \Big|_0^{\frac{-1+\sqrt{10}}{3}}+\dfrac{\pi }{2}\cdot \Big(arcsinx+x\cdot \sqrt{1-x^2}\Big)\Big|_{\frac{1-\sqrt{10}}{3}}^1=\\\\\\=\frac{2\pi \sqrt2}{3\sqrt3}\cdot \sqrt{\frac{(\bf \sqrt{10}-1)^3}{27}}+\frac{\pi }{2}\cdot \left(\frac{\pi }{2} -arcsin\frac{\sqrt{10}-1}{3}-\frac{\sqrt{10}-1}{3}\cdot \sqrt{\frac{2\sqrt{11}-2}{5}}\right)$

Замечание .

$\bf \displaystyle \int \sqrt{1-x^2}\, dx=\Big[\ x=sint\ ,\dx=cost\, dt\ ,\ t=arcsin\, x\ \Big]=\\\\\\=\int \sqrt{1-sin^2t}\cdot cost\, dt=\int cos^2t\, dt=\int \frac{1+cos2t}{2}\, dt=\\\\\\=\frac{1}{2}\int dt+\frac{1}{2}\int cos2t\, dt=\frac{1}{2}\, t+\frac{1}{4}\, sin2t+C=\\\\\\=\frac{1}{2}\, arcsin\, x+\frac{1}{4}\, sin(2arcsin\, x)=\frac{1}{2}\, arcsin\, x+\frac{1}{4}\cdot 2x\sqrt{1-x^2}+C=\\\\\\\frac{1}{2}\, arcsin\, x+\frac{1}{2}\cdot x\sqrt{1-x^2}+C\ ;$